Serie Temporali
Analisi Dati e Statistica, 2025–26
![]()
Università di Trento, Dipartimento di Ingegneria Industriale
Ultimo aggiornamento: 04/12/2025
Serie Temporali
Una serie temporale è costituita da una serie di osservazioni di una variabile aleatoria tale per cui l’influenza di un’osservazione sulle seguenti non possa essere trascurata e—quindi—tale che la dipendenza dal tempo risulti essenziale
Statistica delle serie temporali
Tutti i metodi di regressione visti fin ora sono basati sull’assunzione che la variabile aleatoria sia \(x\overset{IID}\sim \mathcal{N}(\mu, \sigma^2)\). Cioè tutte le osservazioni devono essere non-autocorrelate
Quest’assunzione è, tra l’altro, alla base della raccomandazione di casualizzazione della sequenza operativa
Supponiamo di poter considerare una misura come un segnale tempo-dipendente. È evidente che riducendo l’intervallo di campionamento del segnale prima o poi ogni campione sarà correlato al precedente
Esiste quindi una frequenza di campionamento massima al di sopra della quale ogni misura risulta essere autocorrelata, cioè le osservazioni di \(x\) non sono più IID
Questa situazione sussiste quando la dinamica propria dello strumento di misura o del misurando stesso—che sono sempre finite—sono più lente dell’intervallo temporale in cui si effettuano le misure
Statistica delle serie temporali
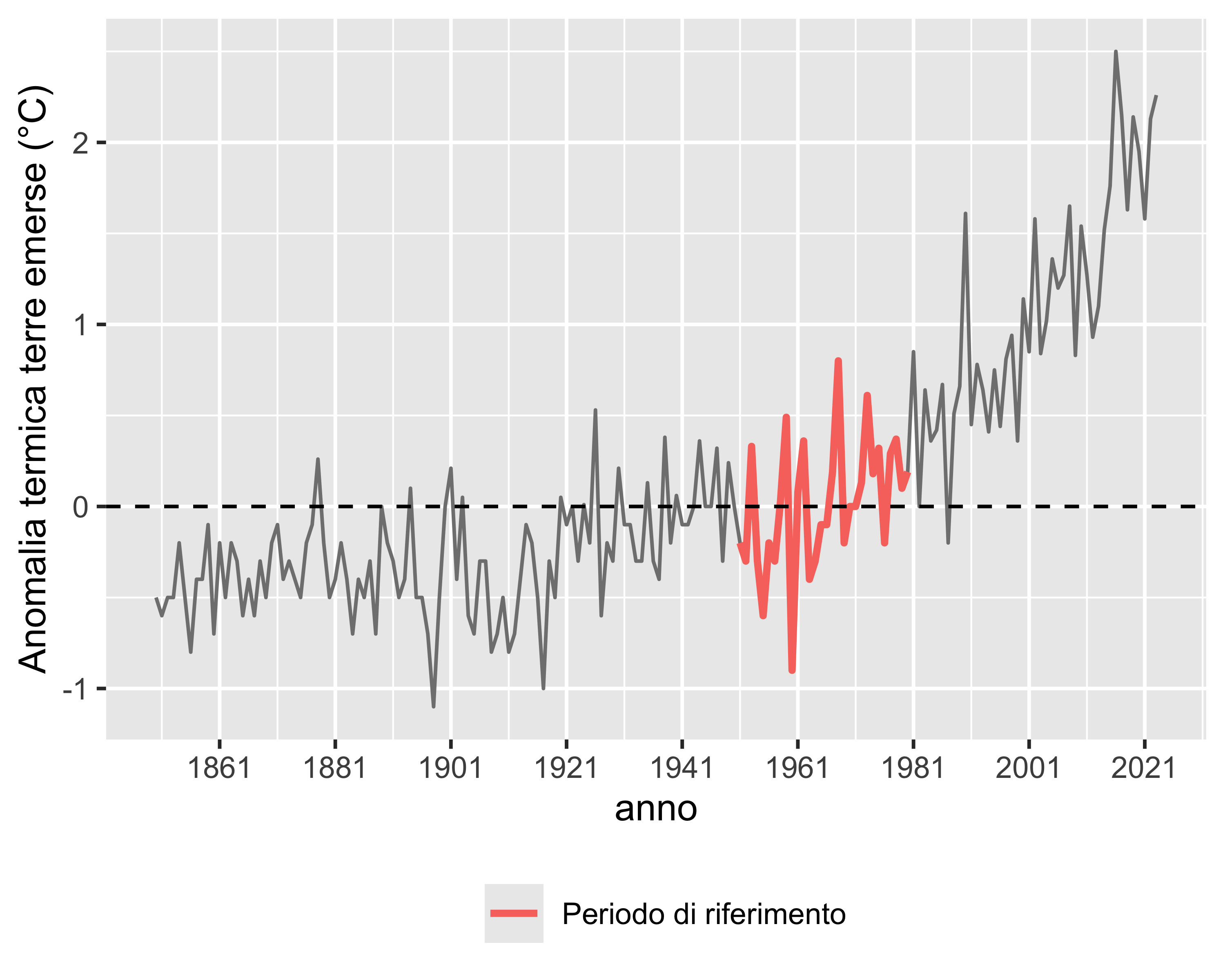
Consideriamo ad esempio la serie temporale in figura che riporta la differenza tra la temperatura media delle terre emerse e il corrispondente valore medio nel periodo 1951–1980
È evidente che osservazioni vicine sono più correlate di osservazioni lontane
Inoltre è evidente (ed è di interesse) valutare la dipendenza della v.a. considerata dal tempo allo scopo di effettuare delle previsioni future
Autocovarianza e autocorrelazione
Abbiamo visto come gli operatori covarianza e correlazione servano a stimare l’indipendenza di due campioni
Considerando un segnale tempo-dipendente \(x=x(t)\), è interessante considerare la covarianza del segnale con se stesso, traslato nel tempo
Definiamo la funzione autocovarianza \(\gamma(s,t)\) come la funzione che valuta la covarianza di un segnale temporale con se stesso valutato iniziando ai tempi \(s\) e \(t\): \[ \gamma_x(s, t) = \sigma_{x_s, x_t} = E[(x_s-\mu_s)(x_t-\mu_t)] \]
È evidente che \(\gamma_x(s,s)=\sigma^2(x_s)\)
La funzione di autocorrelazione (ACF), di conseguenza, è definita come: \[ \rho_x(s, t) = \frac{\gamma_x(s,t)}{\sqrt{\gamma_x(s,s)\gamma_x(t,t)}} \] ed ha il vantaggio di essere sempre compresa in \([-1,1]\). È inoltre evidente che \(\rho_x(s,s)=1\)
Autocorrelazione
Se campioniamo un segnale continuo a intervalli fissi \(\Delta t\) per una durata complessiva \(T\), otteniamo una serie temporale finita di \(N=T/\Delta t\) osservazioni: \(x_{0}=\left<x_1, x_2, \dots, x_N\right>\)
Possiamo estendere la definizione stabilendo che sia \(s=t_0 = 0\) l’istante iniziale della serie e che sia \(t=s+\tau\) un generico momento successivo tale per cui \[ \tau = \ell \Delta t \] dove \(\ell\) è il ritardo o lag, e allora l’autocovarianza e l’autocorrelazione per una s.t. finita risultano: \[ \gamma_x(\ell) = \frac{\sum_{i=1}^{N-\ell} (x_i - \bar x_0) (x_{i+\ell}-\bar x_\ell) }{N-\ell-2},\quad \rho_x(\ell) = \frac{\gamma_x(\ell)}{\sqrt{\sigma_x(0)\sigma_x(\ell)}} \] dove \[ \bar x_0=\frac{1}{N-\ell}\sum\nolimits_{i=1}^{N-\ell} x_i,\quad \bar x_\ell=\frac{1}{N-\ell}\sum\nolimits_{i=\ell}^{N} x_i \]
Autocorrelogramma (ACF)
Per costruire il grafico ACF di una s.t. si trasla l’ascissa di \(\ell\) campioni trascurando i primi \(\ell\) campioni nella s.t. non traslata e gli ultimi \(\ell\) campioni in quella traslata
Poi si calcola l’autocorrelazione tra le due serie
Il processo viene ripetuto per \(\ell=0, 1, \dots, n\), con \(n\) scelto in funzione della dimensione della serie, tipicamente pari ad almeno 50 e comunque non oltre la metà della lunghezza della s.t.
Autocorrelogramma (ACF)
La funzione di autocorrelazione \(\rho_x(\ell)\) che è una funzione a valori discreti, può essere messa in grafico per studiare il lag massimo al di sopra del quale la serie storica \(x\) non è più autocorrelata
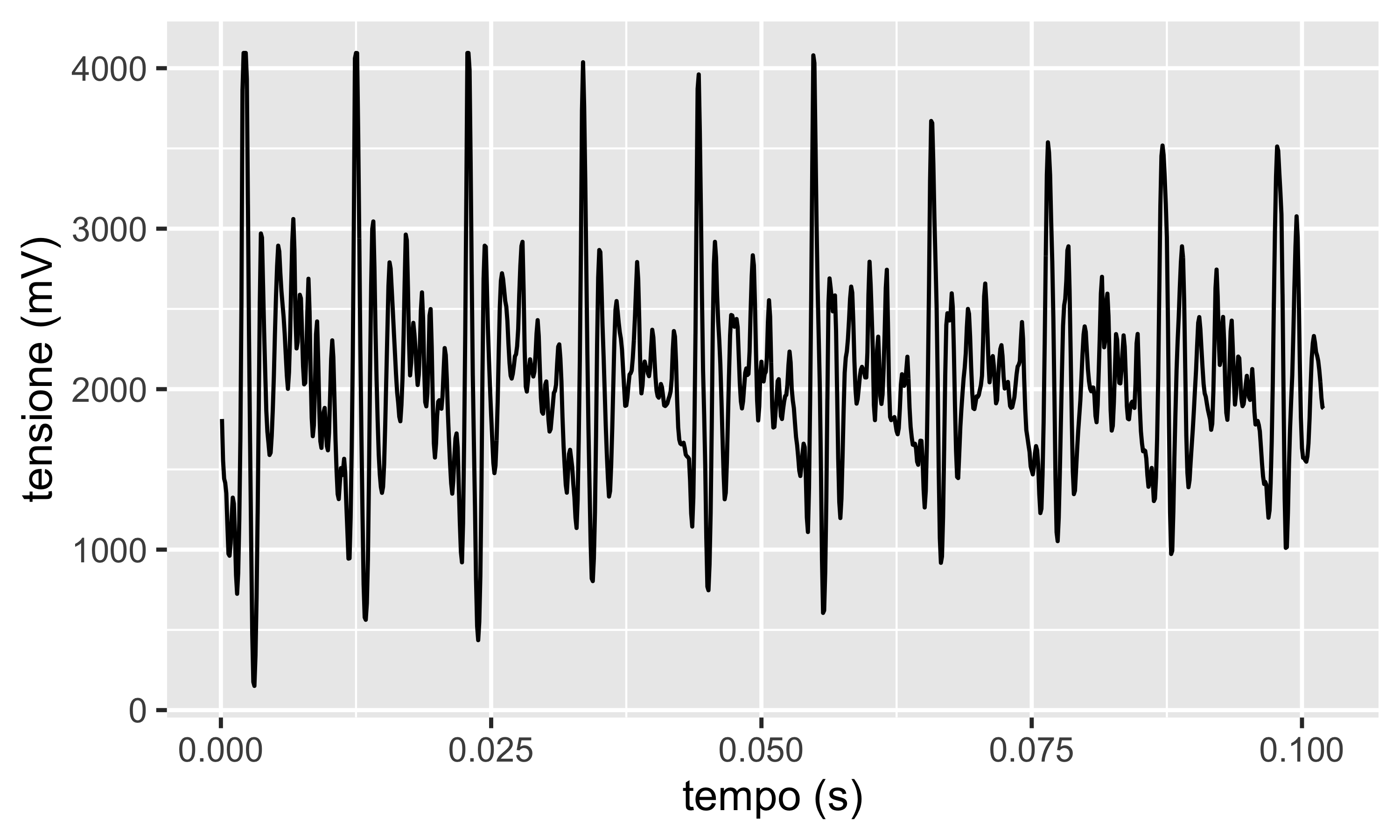
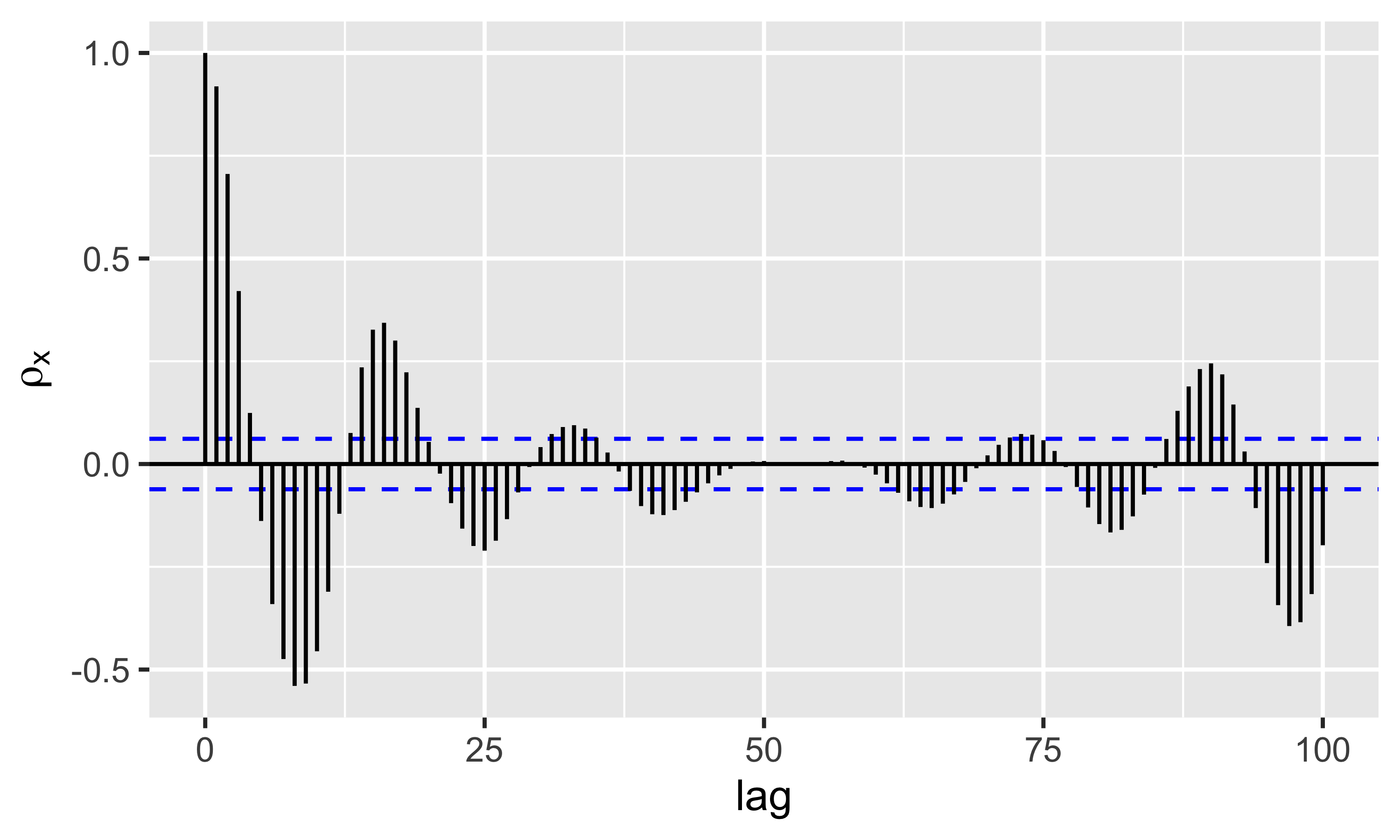
In figura il segnale di un microfono che registra il suono “AAHH”. La serie è evidentemente periodica ogni 0.01 s
L’autocorrelogramma mostra autocorrelazione elevata fino a \(\ell=4\). Poi l’andamento è periodico, a confermare che la s.t. è autocorrelata con se stessa ogni circa 10 lag
Autocorrelogramma (ACF)
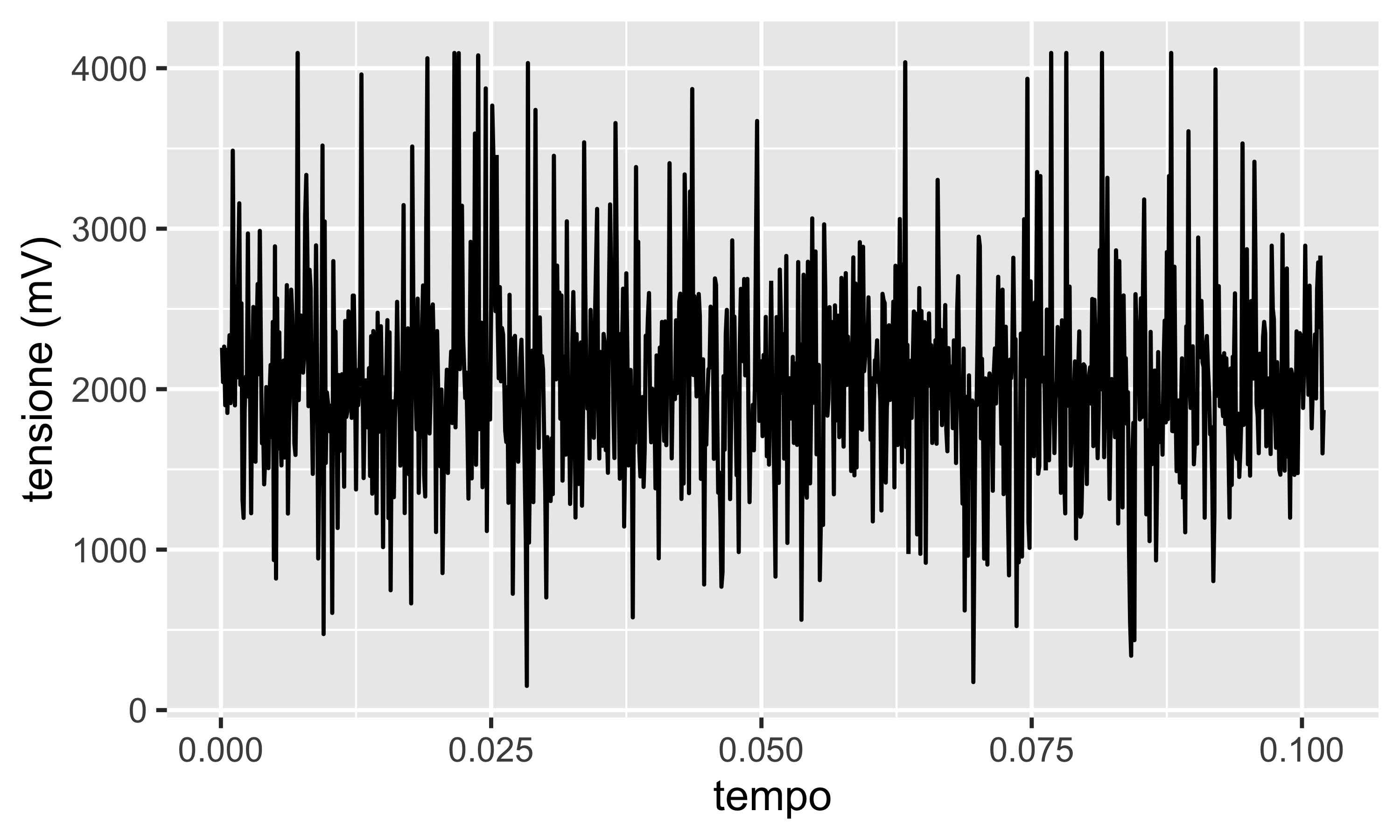
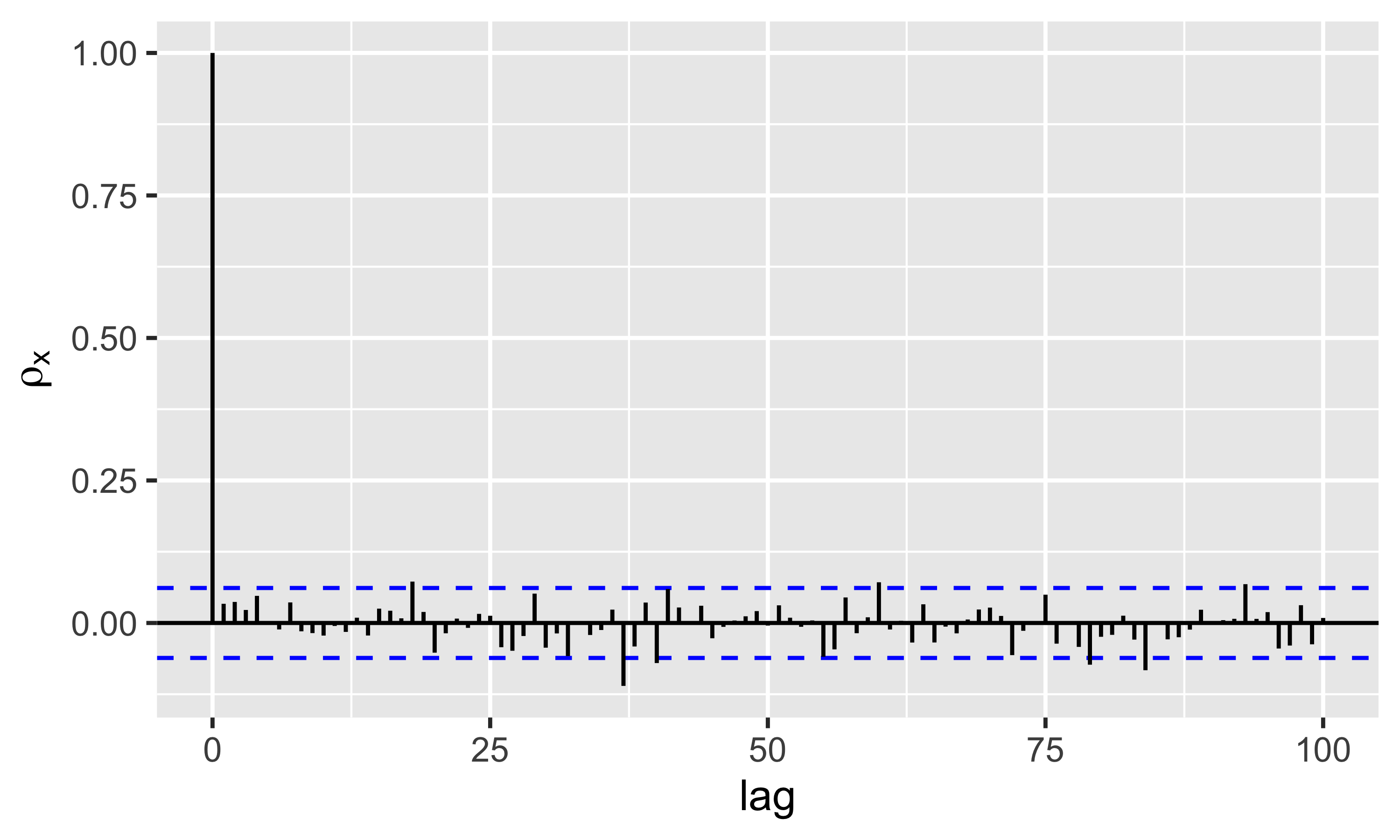
Consideriamo gli stessi dati della s.t. precedente, ma campionati in istanti casuali
Allora \(y\overset{IID}\sim \mathcal{N}(\mu, \sigma^2)\) e quindi \(\rho_y(\ell) = 0~\forall \ell>0\)
Come atteso, l’unico valore della ACF fuori dall’initervallo di confidenza è \(\rho_x(0)\)
In questo caso si dice anche che la s.t. è un random walk
Serie temporali stazionarie
Una s.t. può essere stazionaria o meno. Si definiscono:
- Serie temporale stazionaria in senso ampio
- È una serie temporale per cui il comportamento probabilistico di una qualsiasi collezione di valori \(\left<x_{t_1}, x_{t_2},\dots, x_{t_k}\right>\) è identico a quello della collezione traslata \(\left<x_{t_1+h}, x_{t_2+h},\dots, x_{t_k+h}\right>\), cioè: \[ \mathrm{Pr}(x_{t_1}\leq c_1, \dots, x_{t_k}\leq c_k) = \mathrm{Pr}(x_{t_1+h}\leq c_1, \dots, x_{t_k+h}\leq c_k). \]
- Serie temporale stazionaria in senso stretto
- È una serie temporale per cui il valor medio della serie temporale è costante (tempo-indipendente) e la funzione di autocovarianza \(\gamma(s,t)\) dipende da \(s\) e \(t\) solo tramite la loro differenza \(|s-t|\)
Per una serie stazionaria in senso ampio si può assumere \(\sigma_x(0)=\sigma_x(\ell)=\sigma_x\) e \(\bar x_0=\bar x_\ell\) e, quindi, \(\rho_x(\ell) = \gamma_x(\ell)/\sigma_x\)
Stabilizzazione
- Le ST stazionarie almeno in senso ampio sono più semplici da trattare
- È quindi utile cercare di stabilizzare la ST separandola in un termine di tendenza (trend) \(x_t\) più un termine stazionario \(x_s\)
- la stabilizzazione può essere fatta in due modi:
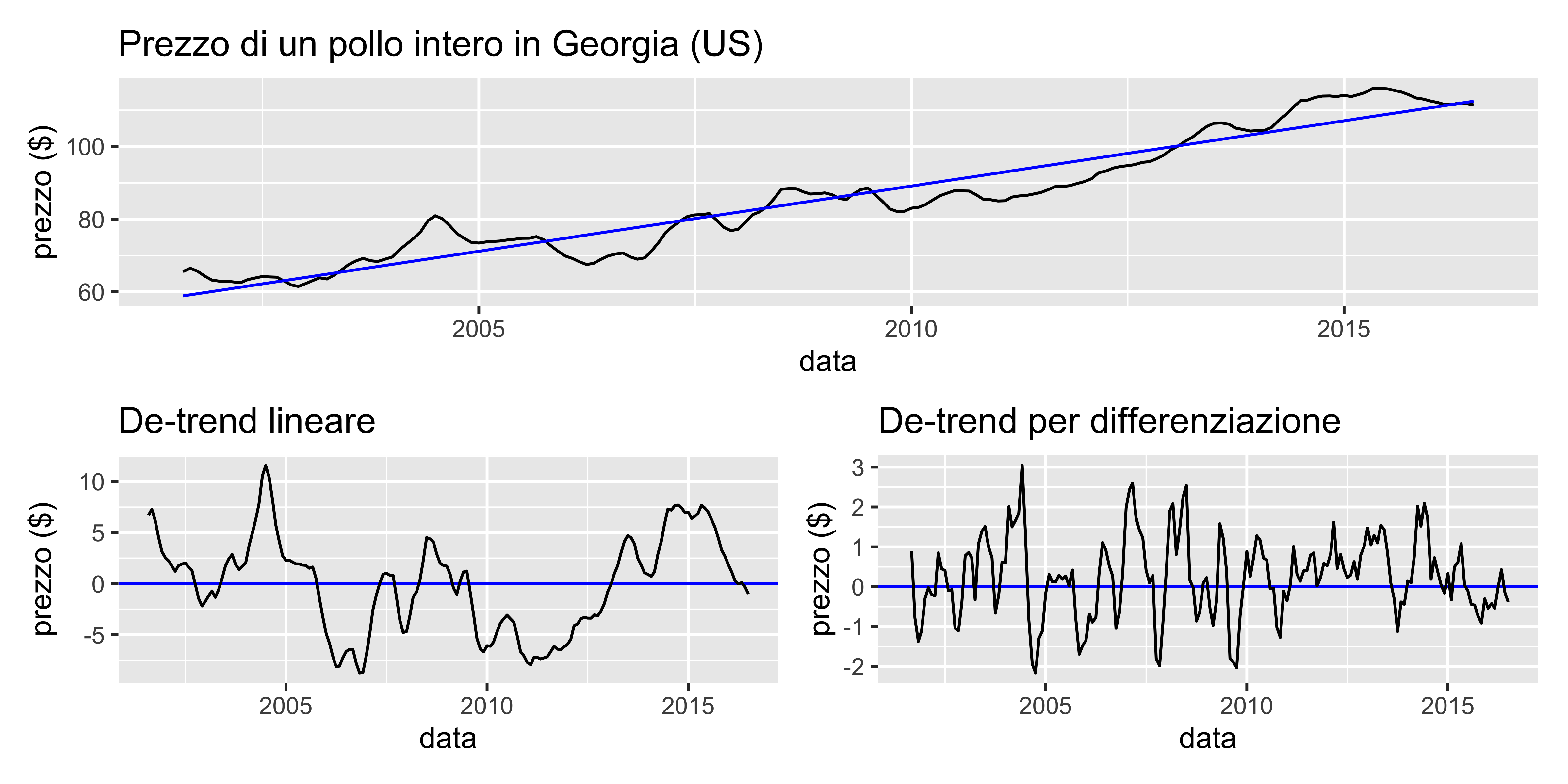
- detrending mediante regressione lineare: \(x_t = x_{l,t} + x_{s,t}\), dove \(x_{l,t} = a + bt\) e, quindi, \(x_{s,t}\) risulta essere la serie dei residui della regressione lineare di \(x_t\)
- detrending per differenziazione
- La ST stabilizzata può poi essere analizzata e quindi ri-trasformata mediante l’operazione inversa:
- somma del termine di tendenza
- integrazione (cioè somma cumulativa)
Stabilizzazione (esempio)
Operatori di differenziazione
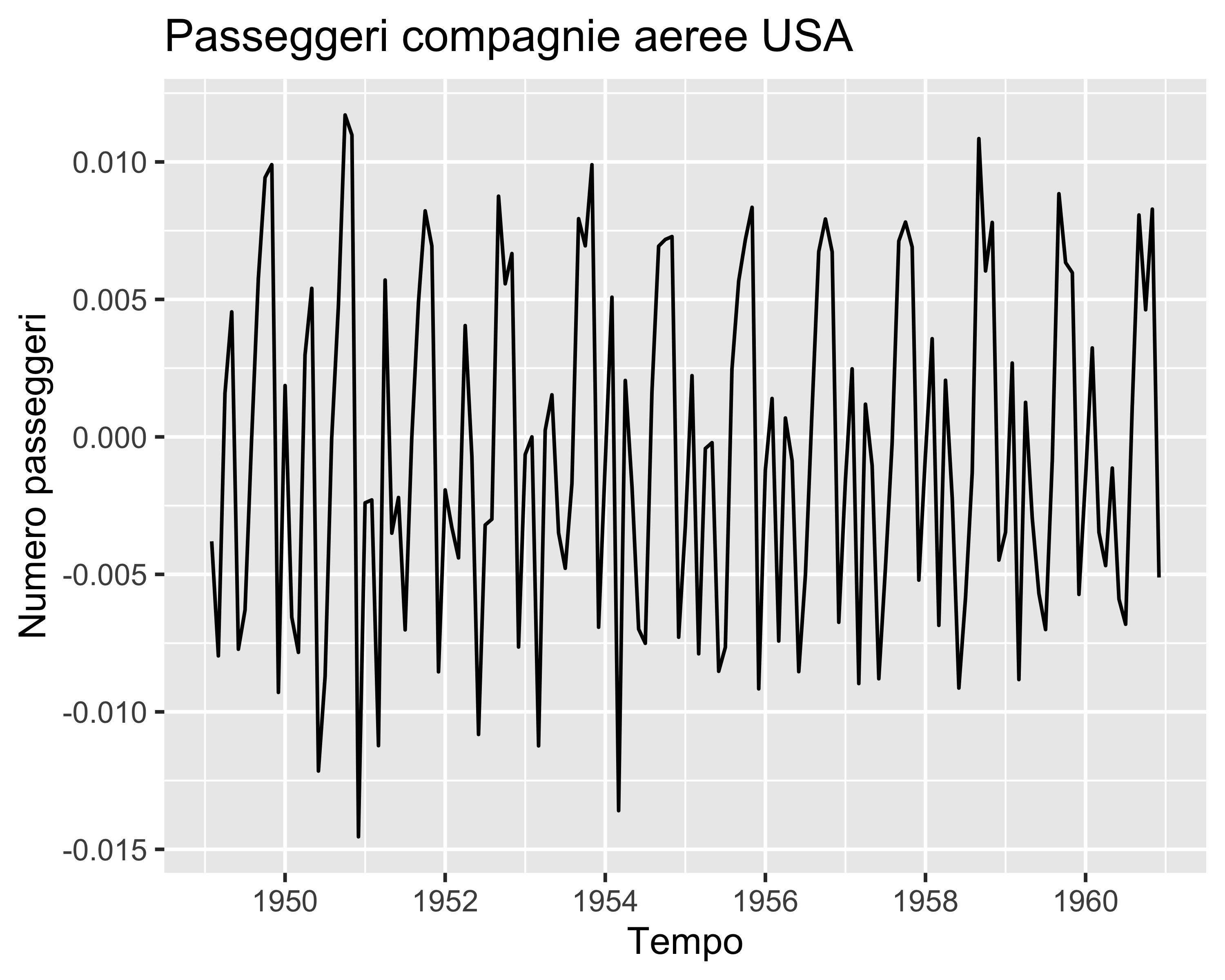
In generale, la stabilizzazione per differenziazione dà risultati migliori ed è anche più pratica: se la ST differenziata non è stabile, è possibile aumentare l’ordine di differenziazione fino a raggiungere la stabilità
Come si differenzia una ST?
Si definiscono:
- Operatore backshift: è l’operatore \(B^n\) tale per cui \(B^n x_t := x_{t-n}\)
- Operatore differenza: è l’operatore \(\nabla\) tale per cui \(\nabla x_t := x_t - x_{t-1}=(1-B)x_t\). Risulta quindi che \(\nabla^dx_t=(1-B)^dx_t\), e quindi ad esempio \(\nabla^2x_t=(1-B)^2x_t=x_t-2x_{t-1}+x_{t-2}\)
Quindi ad esempio la differenziazione \(\nabla^2x_t\) è l’equivalente discreto della derivata seconda \(\frac{d^2}{dt^2}x(t)\) per la funzione continua \(x(t)\)
Stabilizzazione e ACF
Stabilizzazione e ACF
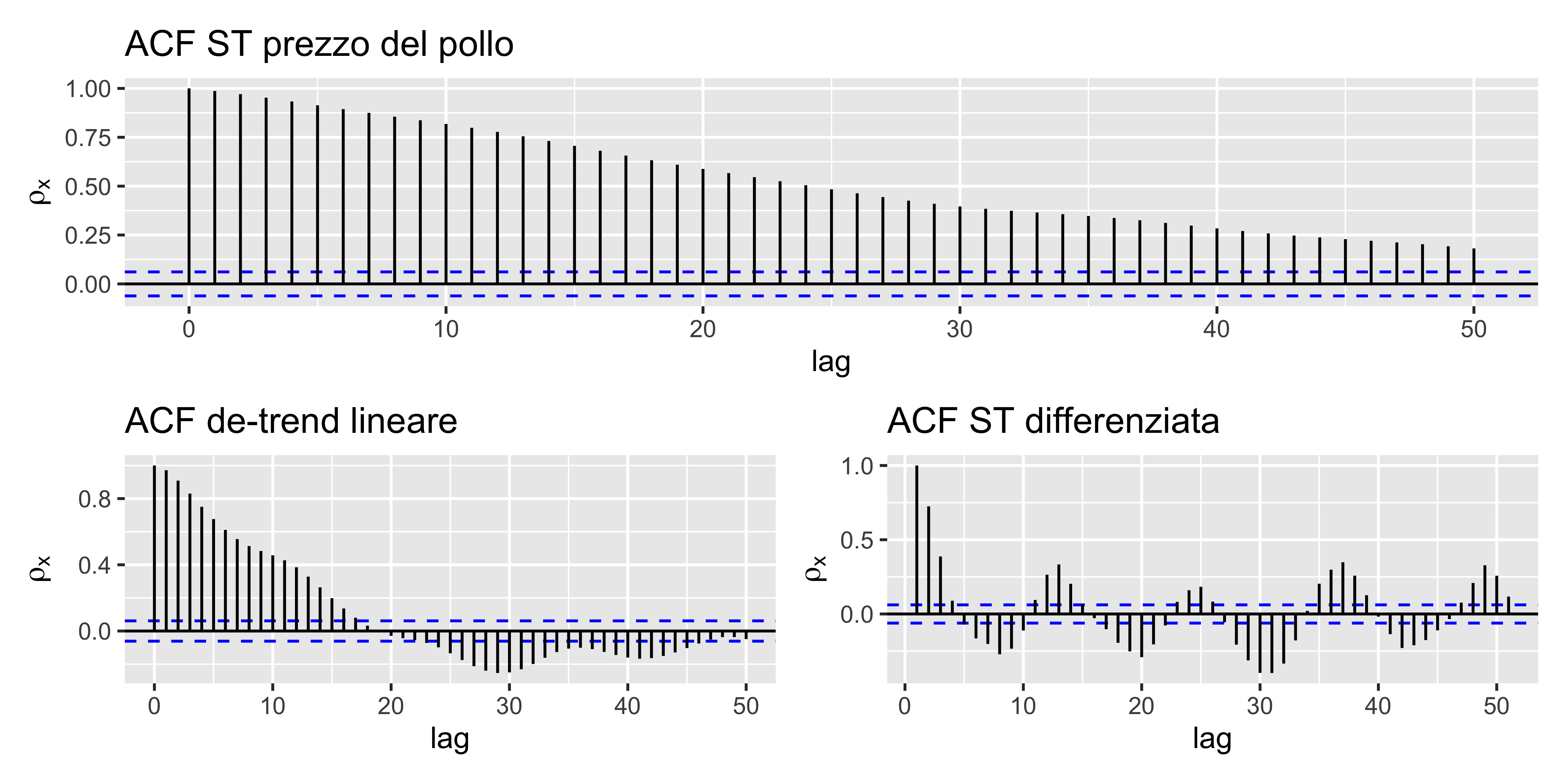
- La ACF di una serie non stabilizzata mostra sempre una correlazione anche a lag elevati
- La ACF della serie dei residui di una regressione lineare decresce più rapidamente, ma mantiene comunque una correlazione anche a lag elevati
- La ACF della serie differenziata, inoltre, si smorza molto rapidamente (i lag 1, 2, 3, … dovrebbero essere esponenziali), dopodiché mostra oscillazioni armoniche, indice di una periodicità nella ST originale
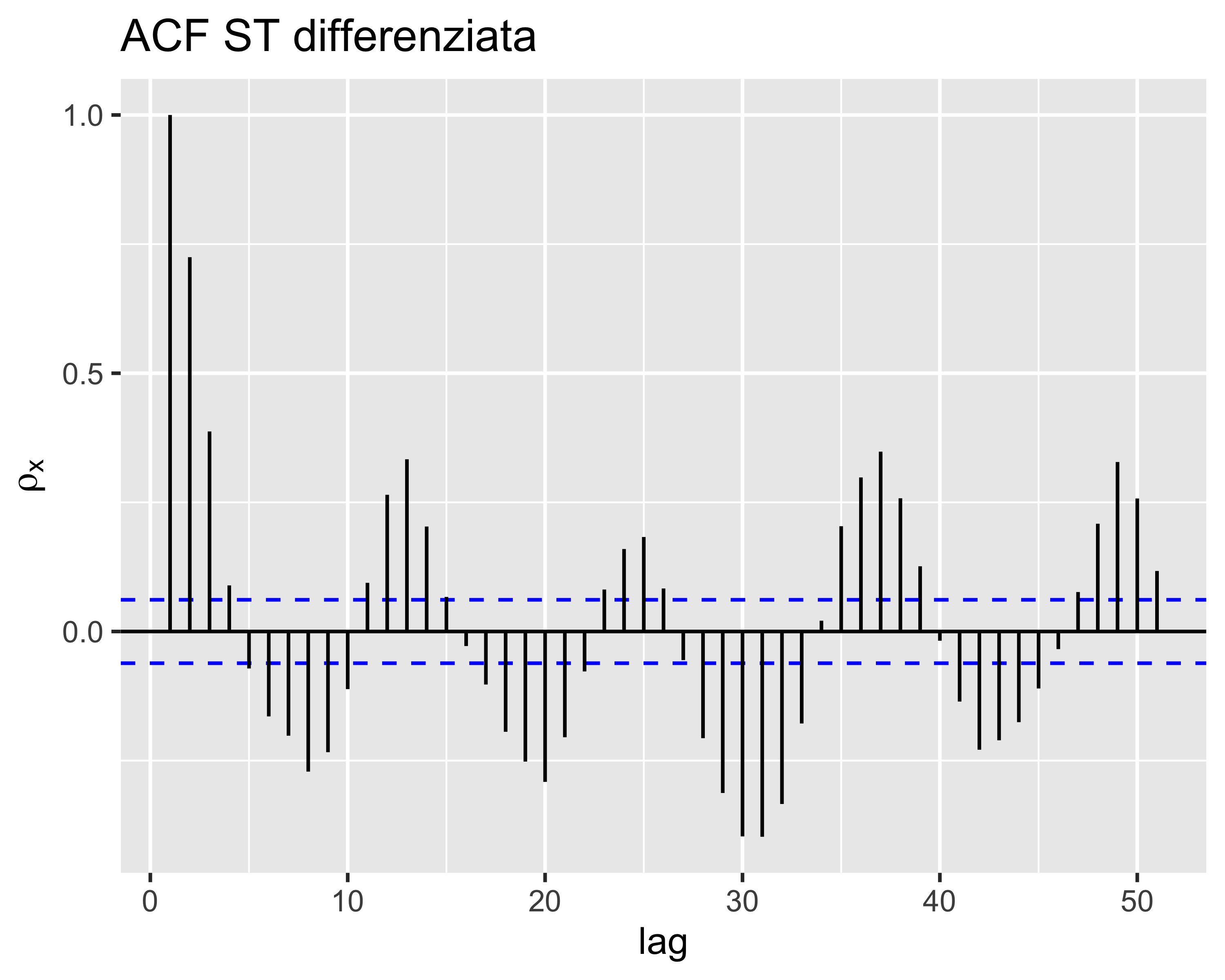
Modelli statistici
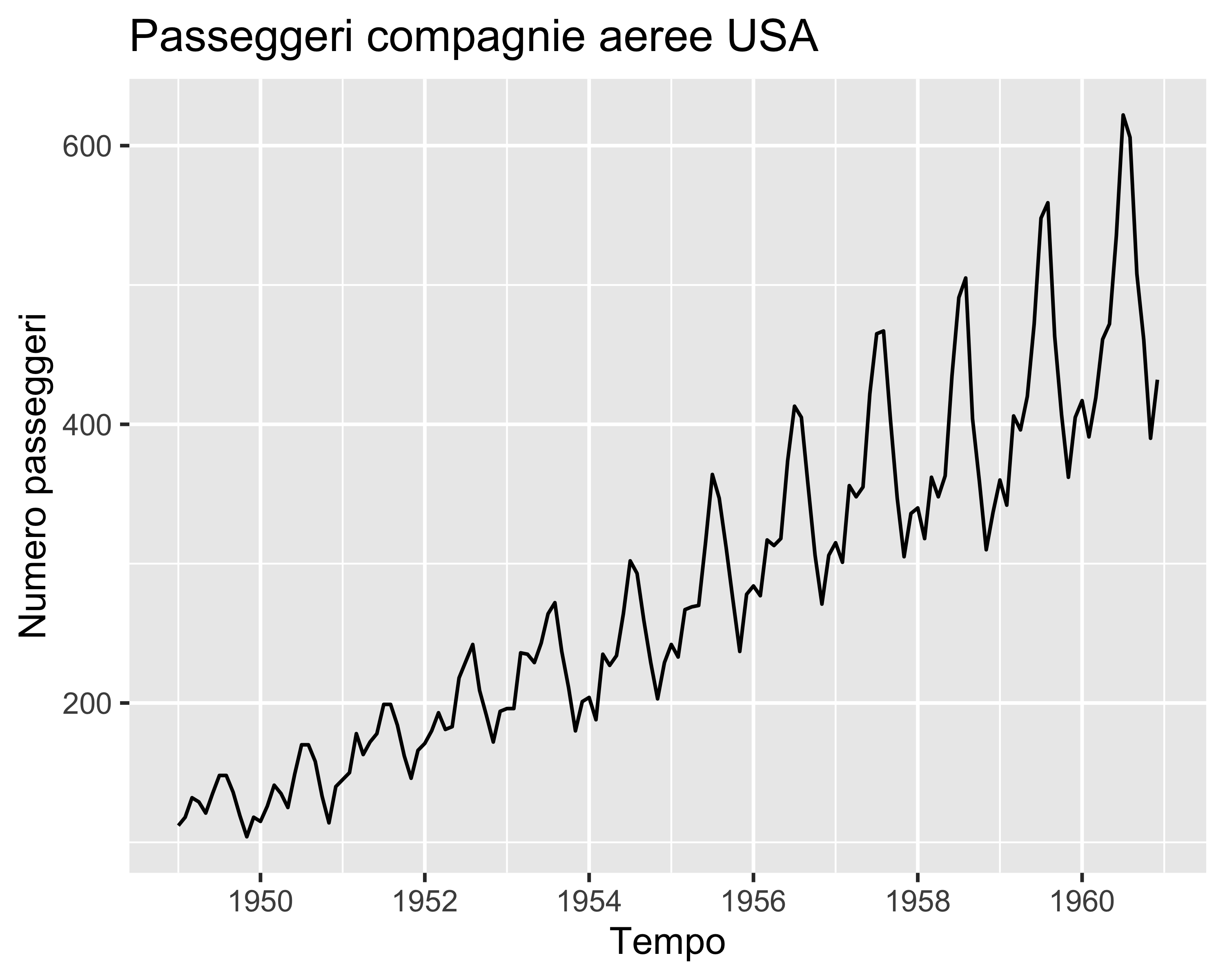
La regressione classica applicata alle serie temporali è spesso insufficiente. Ad esempio, nel caso del prezzo del pollo l’analisi della autocorrelazione mostra un comportamento ciclico che la regressione classica non riesce ad evidenziare
È quindi necessario sviluppare delle tecniche che consentano di modellare i dettagli di una serie temporale, in particolare tenendo in considerazione anche l’autocorrelazione che può caratterizzare le serie temporali
Modelli AR — definizione
Un modello Auto-Regressivo (AR) esprime una determinata osservazione \(x_t\) al tempo \(t\) come combinazione lineare di \(p\) valori precedenti \(x_{t-1}, x_{t-2},\dots,x_{t-p}\). Un modello AR di ordine \(p\), abbreviato in \(\mathrm{AR}(p)\), ha la forma: \[ x_t=\phi_1 x_{t-1} + \phi_2 x_{t-2}+\dots+\phi_p x_{t-p} + w_t \label{eq:AR} \]
- \(x_t\) è stazionaria in senso ampio e \(w_t\sim\mathcal{N}(0, \sigma^2_w)\)
- \(\phi_1, \phi_2,\dots,\phi_p\) sono costanti e \(\phi_p\neq0\)
Se la media di \(x_t\) non è nulla, si sostituisce \(x_t\) con \(x_t - \mu\) per ottenere: \[ \begin{align} x_t-\mu&=\phi_1( x_{t-1}-\mu) + \phi_2 (x_{t-2}-\mu)+\dots+\phi_p (x_{t-p}-\mu) + w_t \\ x_t&=\alpha + \phi_1 x_{t-1} + \phi_2 x_{t-2}+\dots+\phi_p x_{t-p} + w_t,~~~\alpha=\mu(1-\phi_1-\phi_2-\dots-\phi_p) \end{align} \]
Modelli AR — regressione
Ricordando la definizione dell’operatore backshift, la definizione di \(w_t\) può essere scritta come:
\[ (1-\phi_1 B - \phi_2 B^2 -\dots-\phi_p B^p)x_t=w_t \] o ancora più concisamente come:
\[ \Phi_p(B)x_t=w_t \] dove \(\Phi_p(B):=1-\phi_1B-\phi_2B^2-\dots-\phi_pB^p\) è detto operatore autoregressivo.
Effettuare la regressione di un modello \(\mathrm{AR}(p)\) su una serie storica \(x_t\) significa quindi adattare il modello \(\Phi_p(B)\hat{ x_t}=w_t\) identificando i coefficienti di \(\Phi_p(B)\) che minimizzano i residui quadratici medi, essendo i residui \(\varepsilon_t = x_t - \hat{ x_t} = x_t - \Phi_p^{-1}(B)w_t\) (ammesso che esista l’inversa \(\Phi_p^{-1}(B)\)).
Modelli MA — definizione
Alternativamente, è possibile immaginare il caso in cui la generica osservazione \(x_t\) è espressa come combinazione lineare del disturbo agente sulle \(q\) osservazioni precedenti. Un modello MA di ordine \(q\), abbreviato come \(\mathrm{MA}(q)\) è definito come \[ x_t = w_t + \theta_1 w_{t-1} + \theta_2 w_{t-2} + \dots + \theta_q w_{t-q} \]
- \(w_t\sim\mathcal{N}(0, \sigma_w^2)\)
- \(\theta_1, \theta_2,\dots,\theta_q\) sono parametri costanti con \(\theta_q\neq0\)
Modelli MA — regressione
Analogamente al caso \(\mathrm{AR}(p)\), per \(\mathrm{MA}(q)\) è possibile definire l’operatore media mobile di ordine \(q\): \[ \Theta_q(B)=(1+\theta_1 B+\theta_2 B^2+\dots+\theta_q B^q) \] tale per cui la equazione per \(x_t\) può essere scritta come:
\[ x_t=\Theta_q(B)w_t \]
Come sopra, regredire un modello \(\mathrm{MA}(q)\) ad una serie storica \(x_t\) significa identificare i termini di \(\Theta_q(B)\) che minimizzano i residui quadratici medi, definiti come \(\varepsilon_t = x_t - \hat{x_t} = x_t - \Theta_q(B)\) (si noti che questa volta non c’è l’inversa!)
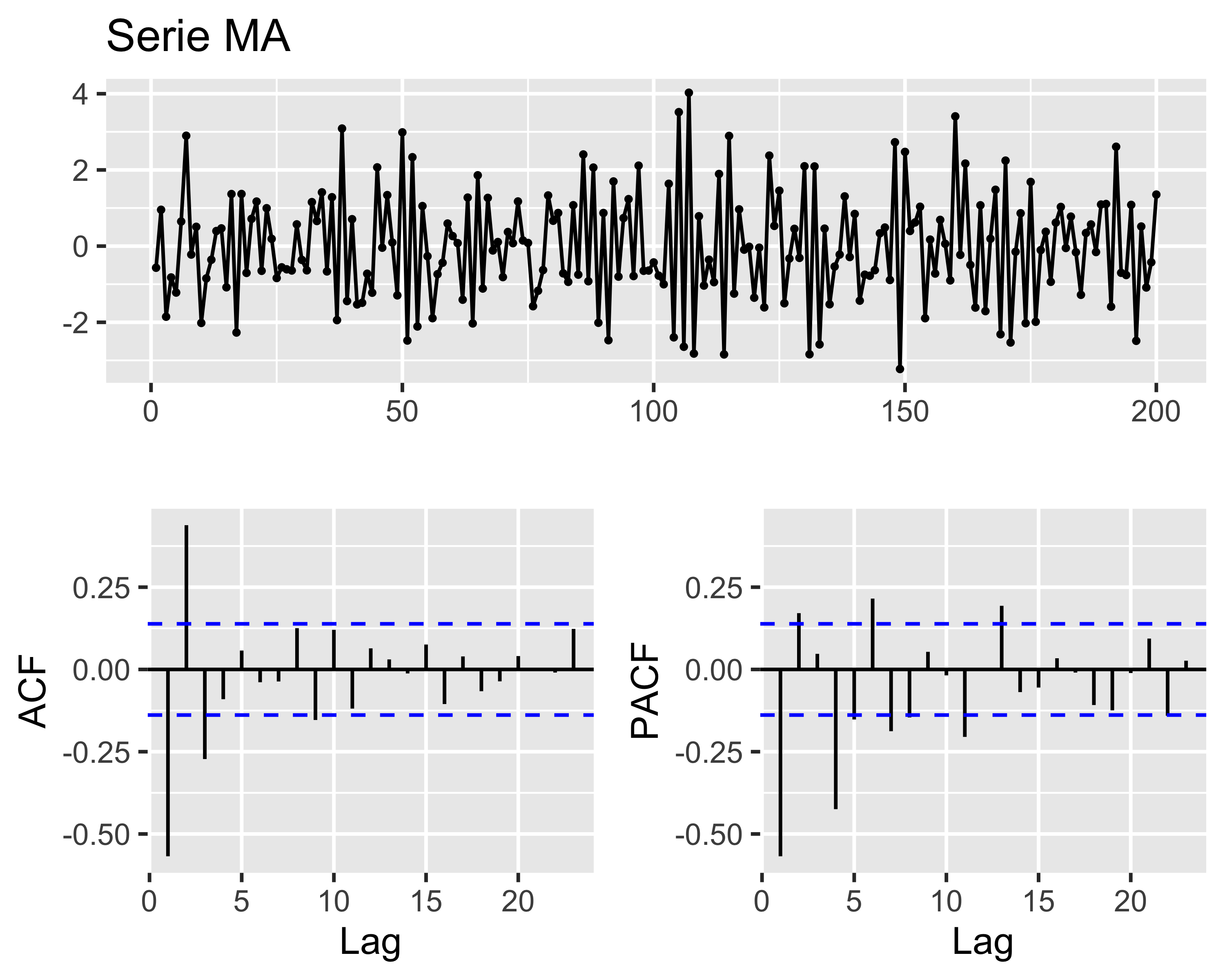
Modelli MA e ACF
Una ST \(MA(q)\) ha una memoria che si estende fino al lag \(q\), nel senso che le innovazioni a distanze superiori a \(q\) non hanno alcun effetto sull’ultima osservazione
Quindi, data una serie temporale di tipo \(MA(q)\) si può spesso identificare l’ordine dalla sua ACF, contando i picchi dopo quello a lag 0:
- tre picchi fuori dalla banda di confidenza significano un modello \(MA(3)\)
- i segni dei picchi corrispondono ai segni dei coefficienti
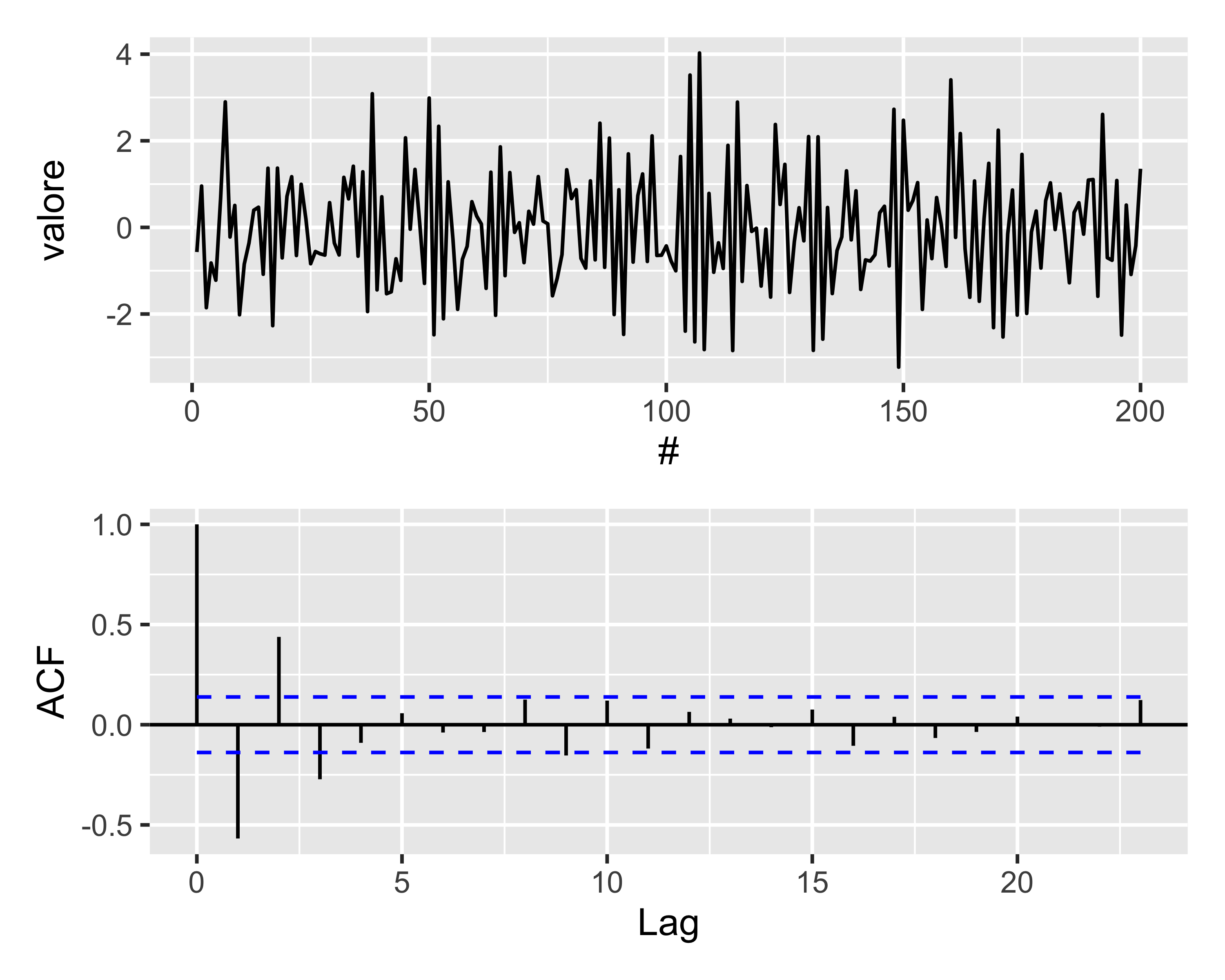
Modelli MA e ACF
Se invece la serie temporale è di tipo \(AR(p)\), ogni osservazione dipende dall’innovazione e da tutte le osservazioni precedenti, in modo ricorsivo
In questo caso l’autocorrelogramma riporterà un decadimento esponenziale seguito eventualmente da oscillazioni armoniche
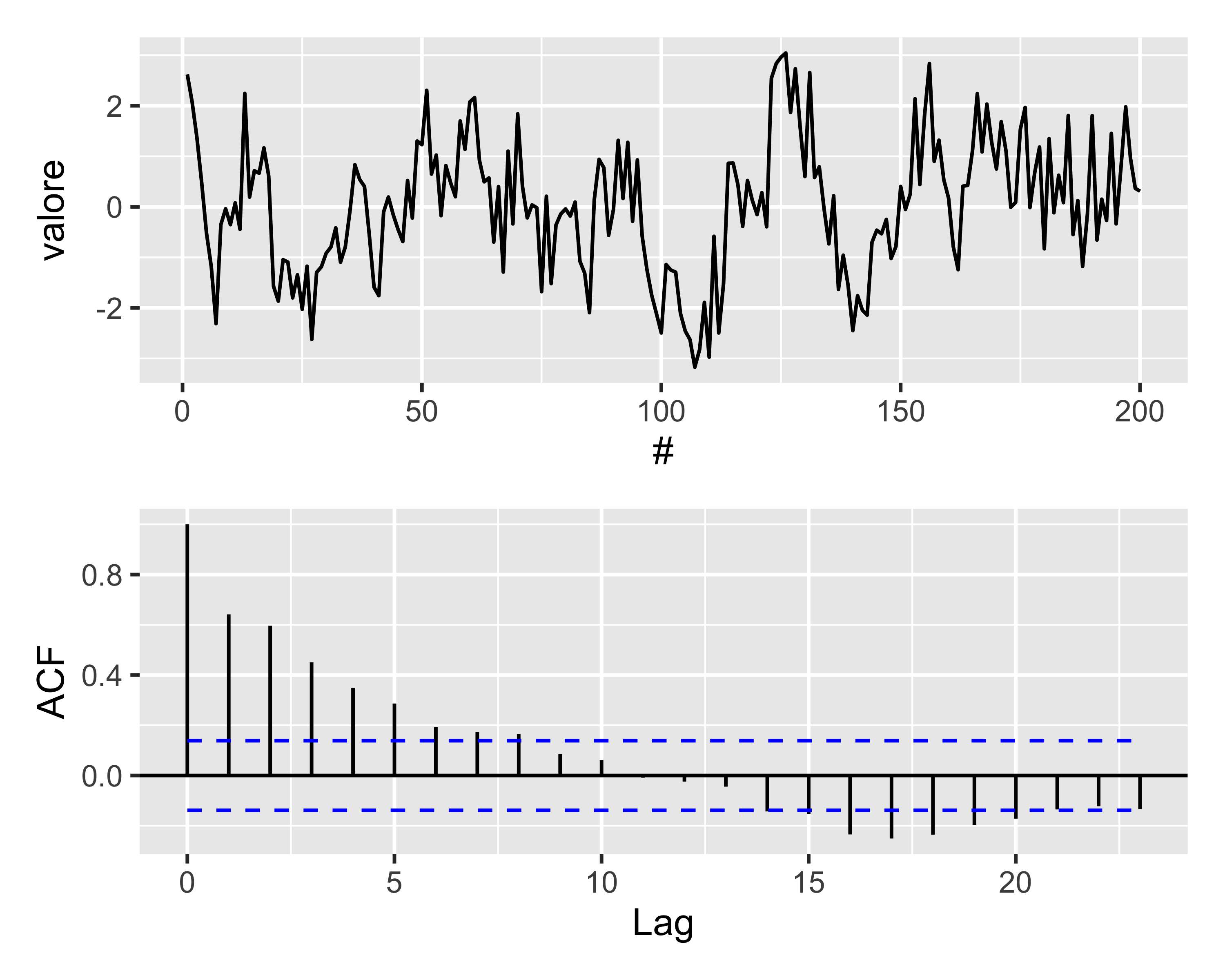
Modelli AR e PACF
Per i modelli di tipo \(AR(p)\) è comunque possibile identificare l’ordine mediante la funzione di autocorrelazione parziale o PACF, così definita:
\[ \begin{align} \mathrm{PACF}_1 &= \mathrm{ACF}(z_{t+1}, z_t) \\ \mathrm{PACF}_k &= \mathrm{ACF}(z_{t+k} - \hat{z_{t+k}}, z_t - \hat{z_t}),~~~k\geq2 \\ \end{align} \] in cui \(\hat{z_{t+k}}\) e \(\hat{z_t}\) sono combinazioni lineari di \(\{z_{t+1}, z_{t+2},\dots,z_{t+k-1}\}\) che minimizzano l’errore quadratico medio di \(z_{t+k}\) e \(z_t\), rispettivamente
Modelli AR e PACF
In generale, quindi, se la ACF mostra una memoria infinita (modello AR) e la PACF mostra pochi picchi, il numero di picchi è l’ordine del modello AR
Attenzione: non si considerano i picchi dopo il primo cut-off, cioè il lag in corrispondenza del quale l’autocorrelazione scende sotto il limite di confidenza per la prima volta
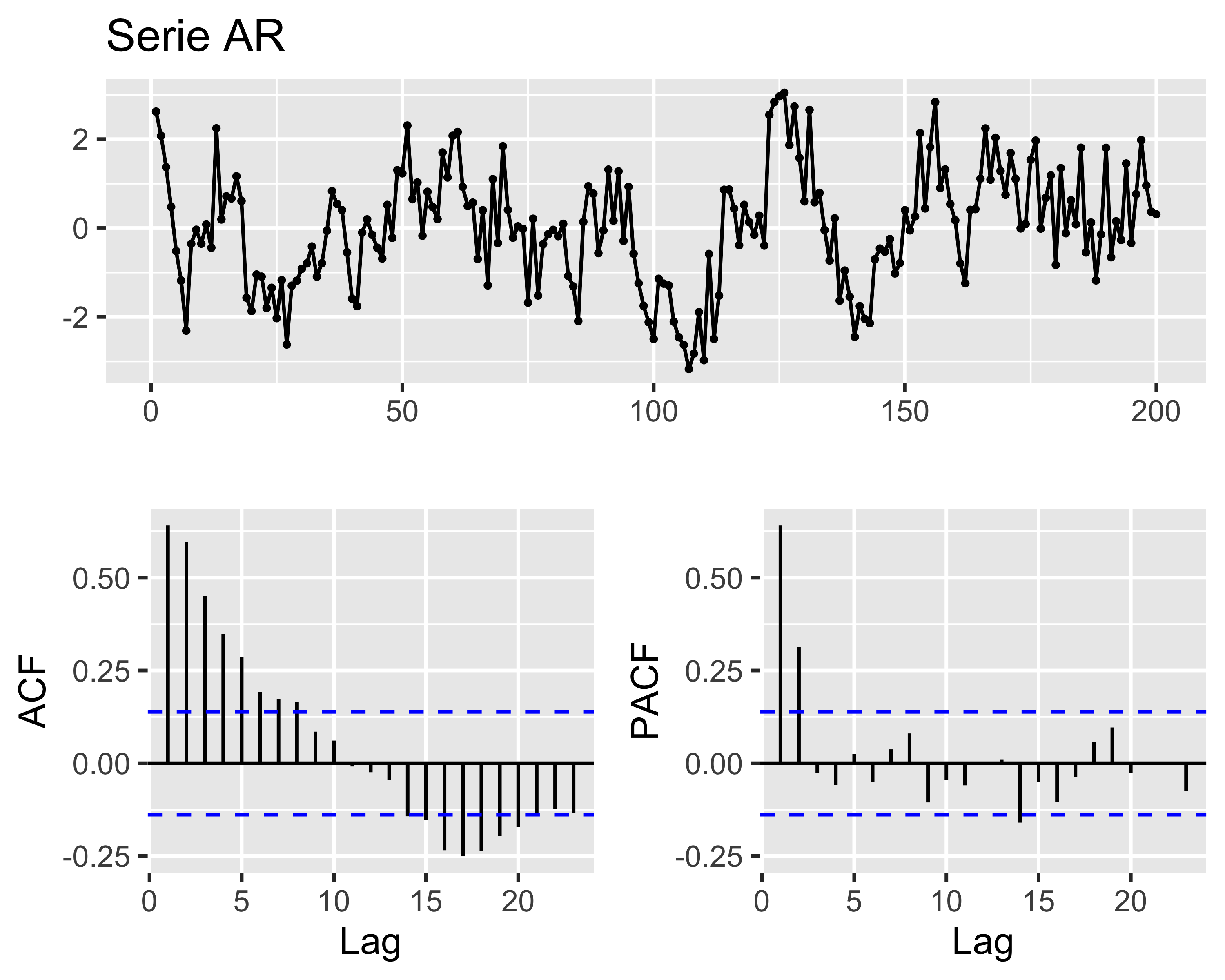
Modelli MA e PACF
Confrontando sia ACF che PACF
- puro rumore: ACF e PACF sono nulle per lag maggiore di 0
- \(AR(p)\): ACF decresce lentamente, PACF non-nulla per lag minori o uguali a \(p\), nulla altrimenti
- \(MA(q)\): ACF mostra \(q\) picchi; se \(PACF(1) > 0\), PACF oscilla a 0, altrimenti decade geometricamente a 0
Modelli ARMA
L’ovvia estensione risulta dalla combinazione dei modelli \(\mathrm{AR}(p)\) e \(\mathrm{MA}(q)\)
Un modello ARMA di ordine \(p,q\), abbreviato come \(\mathrm{ARMA}(p,q)\) è definito come:
\[ x_t=\phi_1 x_{t-1} + \phi_2 x_{t-2}+\dots+\phi_p x_{t-p} + w_t + \theta_1 w_{t-1} + \theta_2 w_{t-2} + \dots + \theta_q w_{t-q} \] con \(\phi_p\) e \(\theta_q\) non nulli, ovvero, più brevemente: \[ \Phi_p(B)x_t=\Theta_q(B)w_t \]
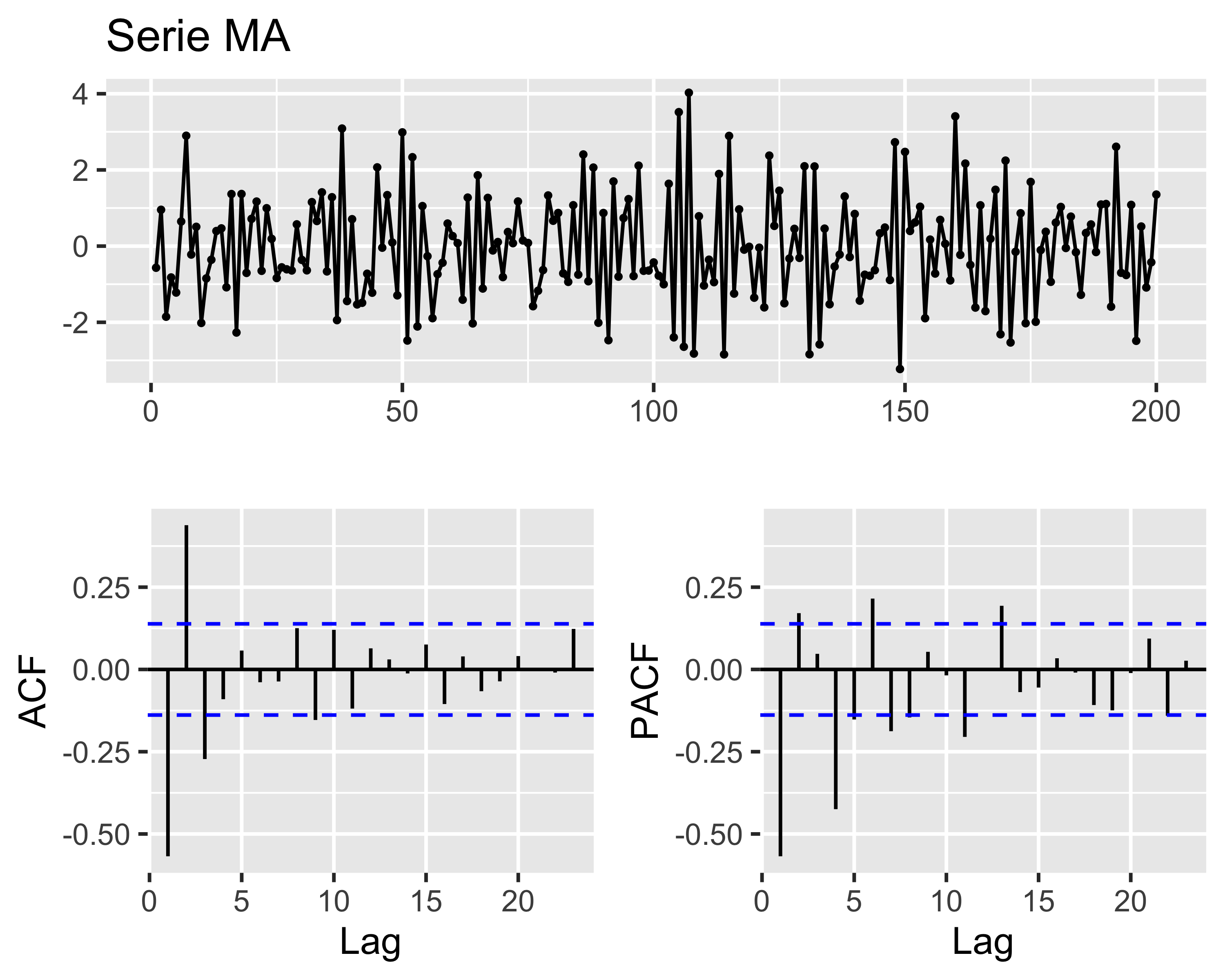
Modelli MA e PACF
Confrontando sia ACF che PACF
- puro rumore: ACF e PACF sono nulle per lag maggiore di 0
- \(AR(p)\): ACF decresce lentamente, PACF non-nulla per lag minori o uguali a \(p\), nulla altrimenti
- \(MA(q)\): ACF mostra \(q\) picchi; se \(PACF(1) > 0\), PACF oscilla a 0, altrimenti decade geometricamente a 0
- \(ARMA(p,q)\): ACF mostra \(q\) picchi; PACF decade geometricamente a 0 solo dopo lag \(p\)
Modelli ARIMA
I processi \(\mathrm{ARMA}(p,q)\) sono adatti solo a descrivere serie stazionarie in senso ampio
Abbiamo visto però che un processo non stazionario può essere reso tale per differenziazione di un opportuno grado \(d\)
Un processo \(x_t\) è detto \(\mathrm{ARIMA}(p,d,q)\) quando \(\nabla^d x_t = (1-B)^d x_t\) 2è un processo \(\mathrm{ARMA}(p,q)\)
In generale, quando \(E(\nabla^dx_t)=0\) il processo \(\mathrm{ARIMA}(p,d,q)\) può essere scritto come: \[ \Phi_p(B)\nabla^dx_t=\Theta_q(B)w_t \] Se invece il valore atteso \(E(\nabla^dx_t)=\mu\), allora: \[ \Phi_p(B)\nabla^dx_t=\delta + \Theta_q(B)w_t,~~~\delta=\mu(1-\phi_1-\dots-\phi_p) \]
Stabilità e unicità dei modelli
Consideriamo un modello \(\mathrm{AR}(1)\): possiamo sviluppare la formula ricorsiva come: \[ \begin{align} x_t =& \phi x_{t-1}+w_t = \phi(\phi x_{t-2}+w_{t-1}) + w_t \\ =& \sum_{j=0}^{+\infty}\phi^j w_{t-j} \end{align} \] È quindi evidente che la serie temporale \(x_t\) è stabile solo se \(|\phi|<1\)
Nel caso generale del modello \(\mathrm{AR}(p)\), si ha la condizione di stabilità: \[ \left|\sum_{i=1}^p \phi_i\right| < 1 \label{eq:ARstab} \] Un modello AR non stabile è detto anche anti-causale, perché si può dimostrare che per essere stabilizzato richiede la conoscenza delle osservazioni future
Stabilità e unicità dei modelli
Per un modello \(\mathrm{MA}(1)\), invece, consideriamo due modelli: \[ \begin{align} x_t &= w_t + \theta w_{t-1}, ~w_t\sim\mathcal{N}(0, 1) \\ y_t &= \nu_t + 1/\theta \nu_{t-1}, ~\nu_t\sim\mathcal{N}(0, \theta^2) \end{align} \] È evidente che \(x_t\) e \(\nu_t\) hanno la stessa ACF e sono indistinguibili, dato che noi non conosciamo le innovazioni \(w_t\) e \(\nu_t\) ma solo le due serie. Si può dimostrare che il risultato è generale (cioè non dipende dell’ordine \(q\)).
È quindi necessario scegliere una delle due forme alternative. Per individuare quale, riscriviamo la serie come \(w_t=-\theta x_{t-1}+x_t\), che ha la stessa forma della \(\mathrm{AR}(1)\). Possiamo quindi scegliere l’alternativa che rispetta lo stesso criterio di stabilità: \[ \left|\sum_{i=1}^q \theta_i\right| < 1 \] Tale alternativa si dice invertibile
Stabilità e unicità dei modelli
In generale, si può dimostrare che i criteri visti sopra corrispondono a imporre il requisito che le radici complesse dei polinomi \[ \begin{align} \Phi_p(z)&=1-\phi_1 z-\phi_2 z^2 - \dots -\phi_p z^p \\ \Theta_q(z)&=1+\theta_1 z+\theta_2 z^2 + \dots +\theta_q z^q \end{align} \] siano tutte strettamente fuori dal cerchio unitario sul piano complesso
Ad esempio: \(\mathrm{ARMA}(2,2)\) con \(\Phi_2(z)= 1 + 0.9z + 0.1z^2\) e \(\Theta_q(z) = 1 + 2z + 15z^2\):
Cioè il termine AR non è causale e il termine MA non è invertibile (ma lo sarebbe \(\theta_q(z) = 1 + 1/2z + 1/15z^2\))
Ridondanza
Consideriamo il processo \(x_t = w_t\), con \(w_t\sim\mathcal{N}(0, 1)\): si tratta ovviamente di puro rumore casuale
Moltiplichiamo entrambi i lati per \(1-0.5B\) per ottenere:
\[ x_t = 0.5x_{t-1}-0.5w_{t-1} + w_t \] che sembra un processo \(\mathrm{ARMA}(1,1)\) ma ovviamente è sempre lo stesso rumore casuale. Come distinguere questi casi?
- si scompongono in fattori i polinomi \(\Phi_p\) e \(\Theta_q\)
- si eliminano i fattori comuni
- si sicompongono i fattori per ottenere il modello non ridondante
In R si può ancora usare polyroot()
Ridondanza
Ad esempio, consideriamo il processo \(x_t=0.4x_{t-1}+0.45x_{t-2}+w_t + w_{t-1}+0.25w_{t-2}\), che usando l’operatore \(B\) diventa:
\[ (1-0.4B-0.45B^2)x_t = (1+B+0.25B^2)w_t. \]
In questa forma il processo sembra \(\mathrm{ARMA}(2,2)\), tuttavia possiamo scomporre i due polinomi in fattori, usando polyroot() per calcolare le radici:
Ridondanza
Come si vede, si può scrivere \[ \begin{align} \Phi_p(B)&=(1-0.9B)(1+0.5B) \\ \Theta_q(B)&=(1+0.5B)^2 \end{align} \]
Eliminando il fattore comune \((1+0.5B)\) otteniamo il modello \[ x_t=0.9x_{t-1}+0.5w_{t-1}+w_t \] che è un \(\mathrm{ARMA}(1,1)\).
Quindi ai criteri di causalità e di invertibilità si aggiunge il criterio di non ridondanza dei parametri, che si verifica eliminando ogni fattore comune dalla scomposizione in fattori dei polinomi \(\Phi_p(B)\) e \(\Theta_q(B)\).
Regressione (S)ARIMA
Per quanto detto sopra, un processo, o serie temporale, \(x_t\) può essere regredita mediante un modello ARIMA identificandone i parametri per minimizzazione degli scarti quadratici
Tuttavia, prima della regressione è necessario definire gli indici \(p, d,q\) adeguati, tali che non si abbia né sotto- né sovra-adattamento
In certi casi, inoltre, le serie sono periodiche: oltre ad un possibile trend sono soggette anche a ciclici andamenti oscillanti. In questi casi:
- si rende la ST stazionaria per differenziazione
- si separa un contributo a bassa frequenza, chiamato stagionale, da un contributo ad alta frequenza
- si effettua separatamente la regressione del contributo stagionale e del contributo non stagionale come due processi ARIMA distinti e sovrapposti: tale regressione si chiama Seasonal ARIMA o SARIMA
Regressione (S)ARIMA
Inoltre, abbiamo visto che i modelli ARIMA si basano sull’ipotesi di serie temporali stazionarie in senso ampio
Quindi, è necessario che sia il valor medio che la varianza siano costanti nel tempo
- La media si stabilizza per differenziazione
- La varianza si può stabilizzare mediante trasformazioni Box-Cox
Quindi, nel caso più generale il modello è \(\mathrm{SARIMA}(p, d, q, p_s, d_s, q_s, \lambda)\)
Prima di eseguire una regressione è quindi necessario definire i valori dei sette parametri, evitando sovra- e sotto-adattamento
- \(d, d_s\) possono essere identificati per tentativi, aumentando gradualmente i valori (prima di \(d\) e poi di \(d_s\)) finché la ACF è soddisfacente
- gli altri termini possono essere individuati verificando la bontà della regressione su una griglia di combinazioni e valutando un opportuno indice di merito
Akaike Information Criterion
L’indice di merito più usato nella regressione SARIMA è l’Akaike Information Criterion, o AIC
In genere la qualità di una regressione con \(k\) parametri è misurata dalla somma quadratica dei residui, \(SS_E(k)\), normalizzata per la dimensione del campione \(n\): \[ \hat{\sigma_k^2} = \frac{SS_E(k)}{n} \] Questo indicatore si chiama Maximum Likelihood Estimator (MLE). Più questo valore è piccolo, meglio il modello si adatta ai dati
Tuttavia aumentando \(k\) si ha una diminuzione di MLE, a rischio di sovra-adattamento. Per questo motivo Akaike ha proposto di penalizzare MLE con il numero di parametri: \[ \mathrm{AIC}=\log(\hat{\sigma_k^2})+\frac{n+2k}{n} \] L’AIC va ovviamente minimizzato
Altri criteri di informazione
Oltre all’AIC esistono anche l’AIC corretto e il Bayesian Information Criterion, o BIC:
- AIC corretto: \(\mathrm{AIC}_c = \log(\hat{\sigma_k^2})+\frac{n+k}{n-k-2}\)
- BIC: \(\mathrm{BIC} = \log(\hat{\sigma_k^2})+\frac{k\log(n)}{n}\)
Il BIC penalizza maggiormente la dimensione del modello, per cui è preferito per campioni molto grandi (migliaia di osservazioni), per i quali AIC e AICc tenderebbero a favorire modelli inutilmente complessi (troppi parametri, sovra-adattamento)
Come l’AIC, anche AICc e BIC vanno minimizzati
Regressione
La libreria R forecast fornisce la funzione auto.arima() che valuta gli indicatori su una griglia di combinazioni dei sette parametri e fornisce la regressione migliore:
ARIMA(2,1,2)(1,1,1)[12] : -890.0518
ARIMA(0,1,0)(0,1,0)[12] : -845.0766
ARIMA(1,1,0)(1,1,0)[12] : -885.6939
ARIMA(0,1,1)(0,1,1)[12] : -896.9901
ARIMA(0,1,1)(0,1,0)[12] : -860.1426
ARIMA(0,1,1)(1,1,1)[12] : -895.2944
ARIMA(0,1,1)(0,1,2)[12] : -895.3558
ARIMA(0,1,1)(1,1,0)[12] : -889.5331
ARIMA(0,1,1)(1,1,2)[12] : Inf
ARIMA(0,1,0)(0,1,1)[12] : -880.0685
ARIMA(1,1,1)(0,1,1)[12] : -896.1031
ARIMA(0,1,2)(0,1,1)[12] : -895.698
ARIMA(1,1,0)(0,1,1)[12] : -893.2768
ARIMA(1,1,2)(0,1,1)[12] : -894.0835
Best model: ARIMA(0,1,1)(0,1,1)[12] Series: AirPassengers
ARIMA(0,1,1)(0,1,1)[12]
Box Cox transformation: lambda= -0.2947046
Coefficients:
ma1 sma1
-0.4355 -0.5847
s.e. 0.0908 0.0725
sigma^2 = 5.856e-05: log likelihood = 451.59
AIC=-897.18 AICc=-896.99 BIC=-888.55Previsione
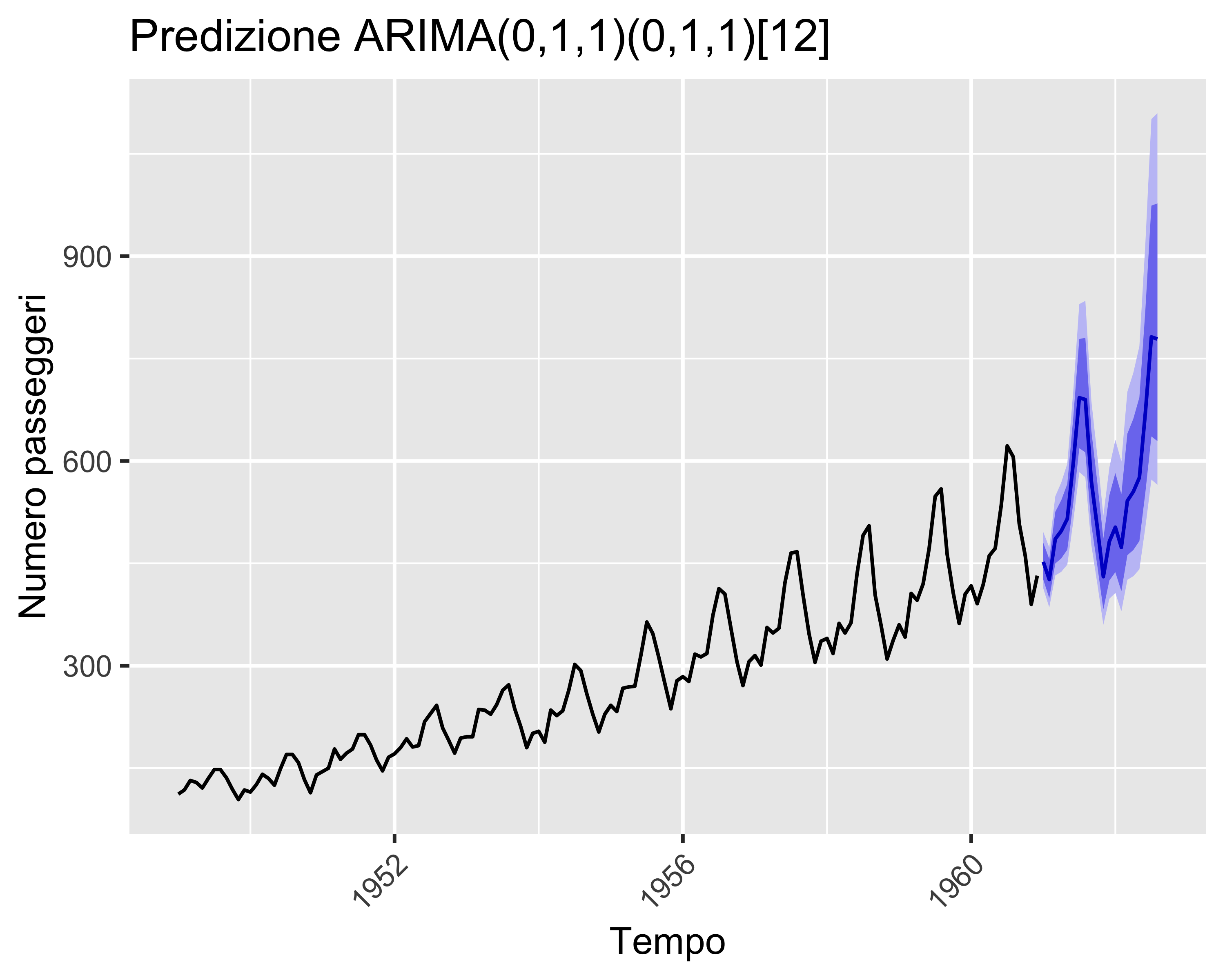
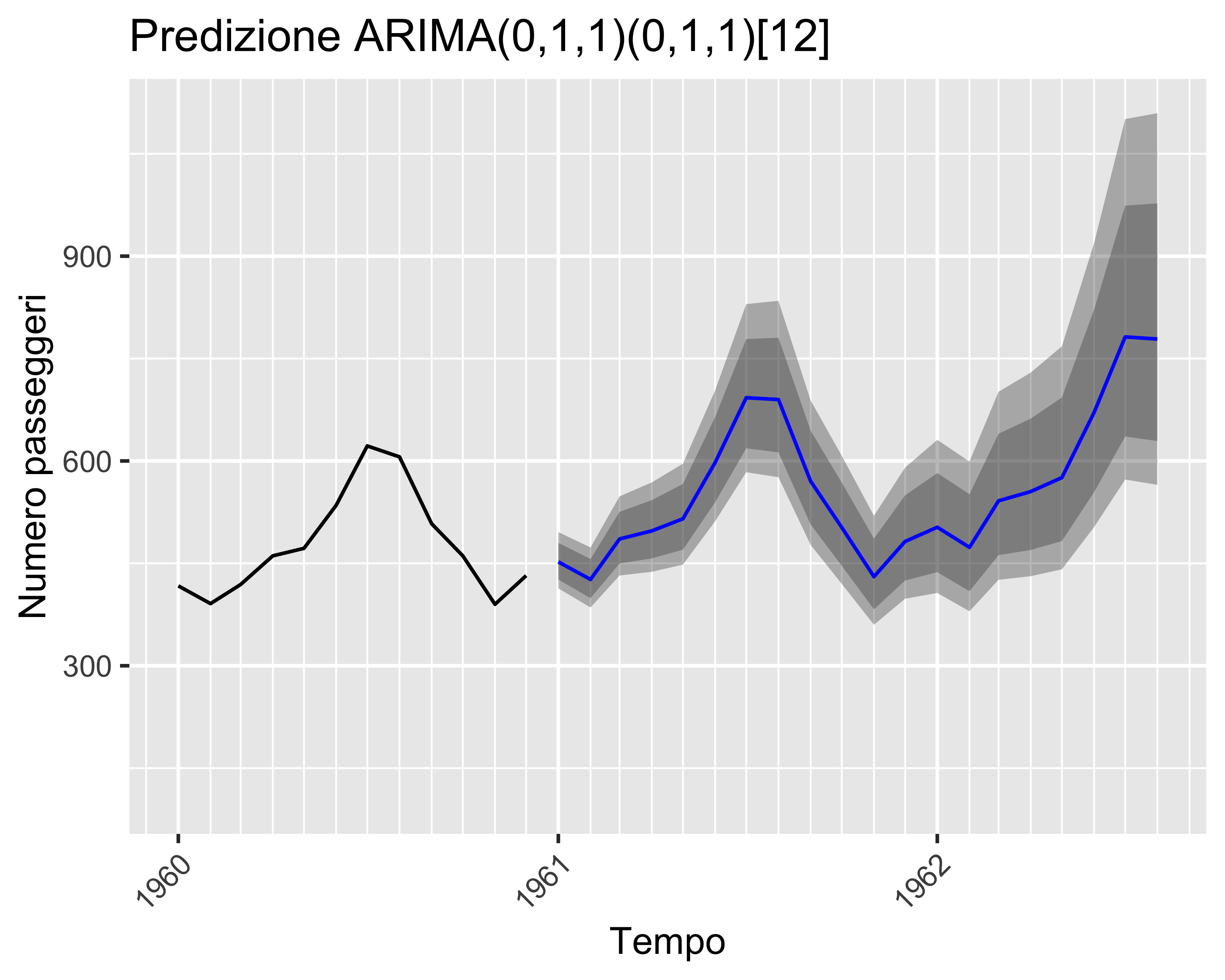
Una volta selezionato il modello più adatto (quello con AIC minimo) si può procedere a regressione e predizione
La predizione può essere ottenuta con la funzione forecast()
Tale funzione riporta anche le bande di confidenza al 95%
paolo.bosetti@unitn.it — https://paolobosetti.quarto.pub/slides/ADAS/