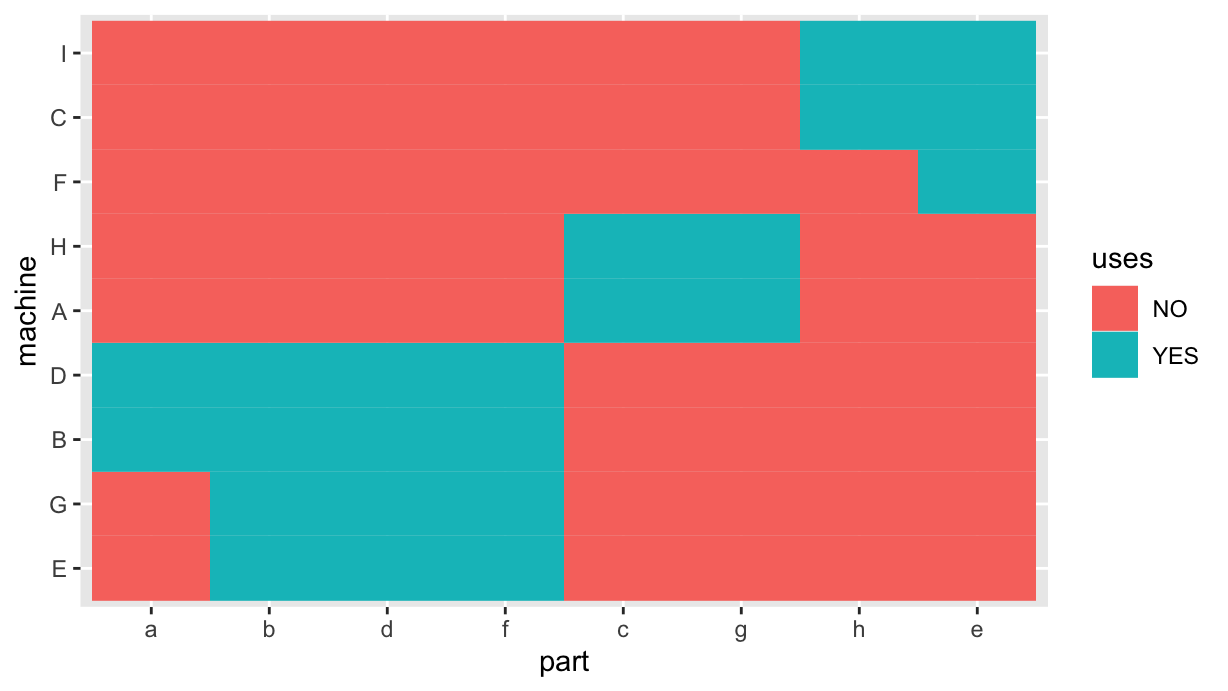
set.seed(0)
m <- matrix(
c(
1, 1, 1, 1, 0, 0, 0, 0,
1, 0, 1, 1, 0, 0, 0, 0,
1, 0, 1, 1, 0, 0, 0, 0,
1, 1, 1, 1, 0, 0, 0, 0,
0, 0, 0, 0, 1, 1, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0,
0, 0, 0, 0, 1, 1, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1,
0, 0, 0, 0, 0, 0, 1, 1
) %>% as.logical(),
ncol=8,
byrow=TRUE
)
m <- m[sample(nrow(m)),sample(ncol(m))]
dimnames(m) <- list(LETTERS[1:nrow(m)], letters[1:ncol(m)])
m a b c d e f g h
A FALSE FALSE TRUE FALSE FALSE FALSE TRUE FALSE
B TRUE TRUE FALSE TRUE FALSE TRUE FALSE FALSE
C FALSE FALSE FALSE FALSE TRUE FALSE FALSE TRUE
D TRUE TRUE FALSE TRUE FALSE TRUE FALSE FALSE
E FALSE TRUE FALSE TRUE FALSE TRUE FALSE FALSE
F FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE
G FALSE TRUE FALSE TRUE FALSE TRUE FALSE FALSE
H FALSE FALSE TRUE FALSE FALSE FALSE TRUE FALSE
I FALSE FALSE FALSE FALSE TRUE FALSE FALSE TRUE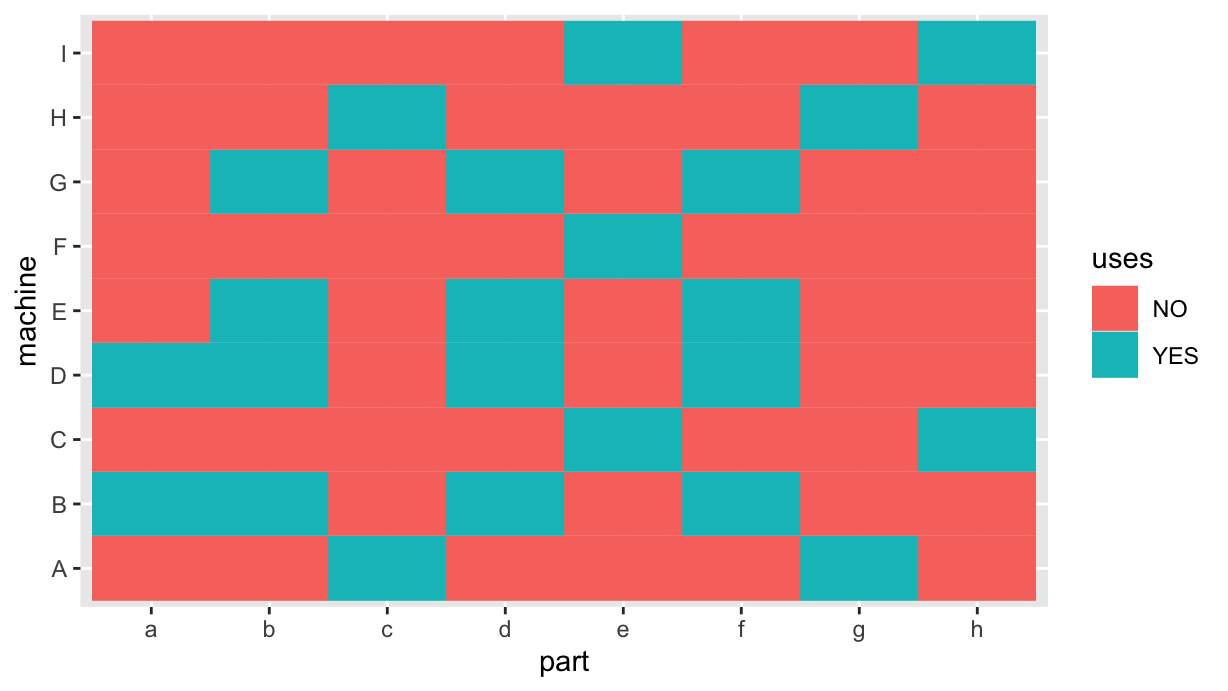
 A Roc is also a huge mythological bird…
A Roc is also a huge mythological bird…