Strumenti di misura

Analisi Dati e Statistica, 2025–26

Paolo Bosetti

Università di Trento, Dipartimento di Ingegneria Industriale

Ultimo aggiornamento: 04/12/2025

Catena di misura

È un sistema composto da una serie di strumenti collegati che elaborano un segnale per ottenere una misurazione

Definizioni

• misurando: oggetto fisico della misurazione
• trasduttore: dispositivo che converte una grandezza fisica in un’altra
• condizionatore: dispositivo che migliore il segnale fisico prodotto dal trasduttore
• conversione AD: trasforma un segnale analogico in un segnale digitale
• acquisizione: opera sul segnale digitale (visualizzazione, registrazione, elaborazione, ecc.)

Esempio: misura estensimetrica

Catena di misura: da deformazione elastica a misura numerica digitalizzata

Trasduttori di posizione

Cioè come rilevare la posizione di un oggetto mobile

Trasduttore capacitivo

La capacità è espressa da: \(C=\varepsilon_r A/d\)

• adatto per misure di spostamento con \(d\) molto piccolo e elevata sensibilità (ordine dei nanometri)
• non è lineare (varia con \(1/d\))
• elevata impedenza, quindi necessita di schermatura
• sensibile a \(\varepsilon_r\) (temperatura, umidità)

Capacitore

Trasduttore induttivo diretto

Sfruttando la variazione di induttanza che risulta da uno spostamento dell’armatura:

• Semplice
• Sensibile a effetti ambientali

Induttanza variabile

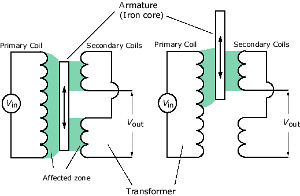
Trasduttore induttivo differenziale

Linear Variable Differential Transformer: sfrutta la differenza tra due avvolgimenti secondari per movimenti opposti del core:

• più complesso e costoso
• auto-compensato per gli effetti ambientali
• più sensibile

LVDT

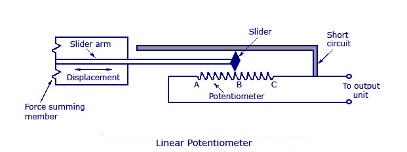
Trasduttore resistivo

Sfrutta una variazione di resistenza in un circuito parallelo \(R_{T} = (1-\Delta)R_v \frac{1}{\Delta R_v + R_{sc}}\)

• economico
• corse discretamente lunghe
• usura
• misura rumorosa

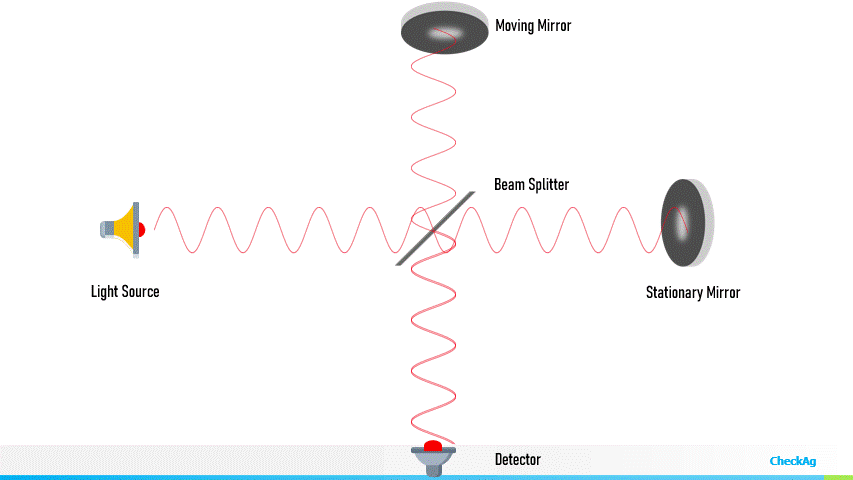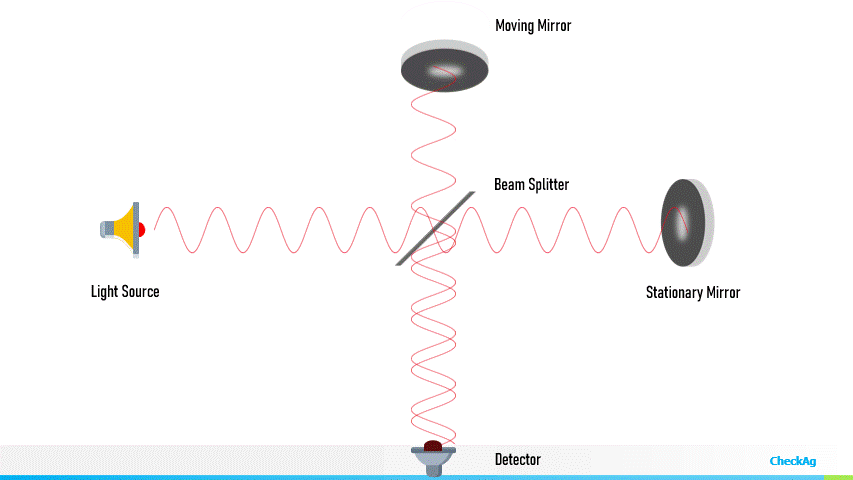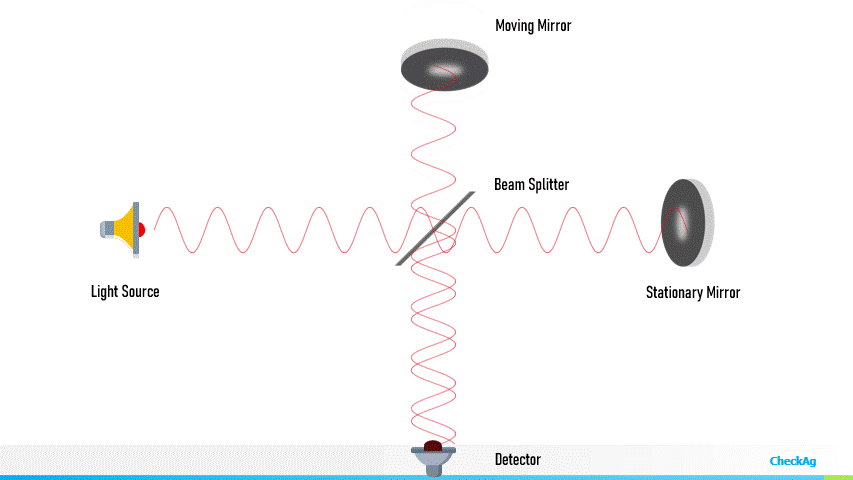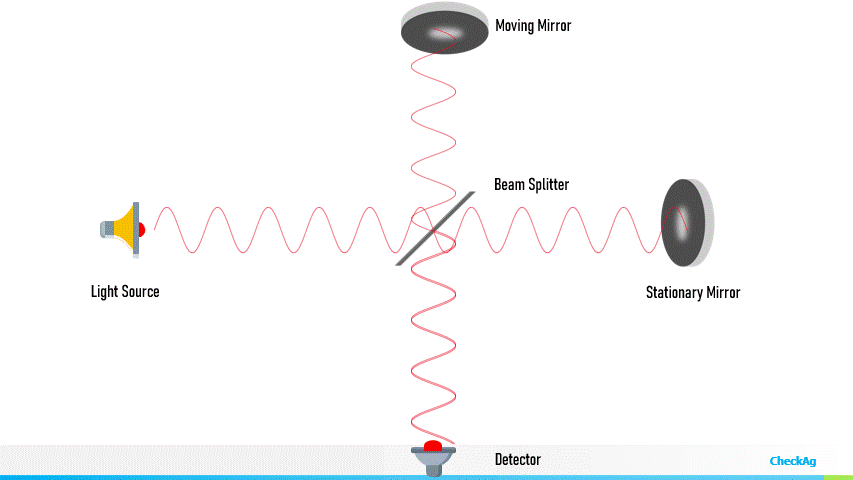
Trasduttore interferometrico

È basato su un conteggio di oscillazioni su una misura di intensità luminosa

• Risoluzione almeno nanometrica, dell’ordine della lunghezza d’onda
• Lunghezze molto grandi (nel vuoto anche milioni di kilometri)
• Sensibile alle proprietà ottiche del mezzo (funzione della temperatura e umidità, se è aria)

Interferometria laser

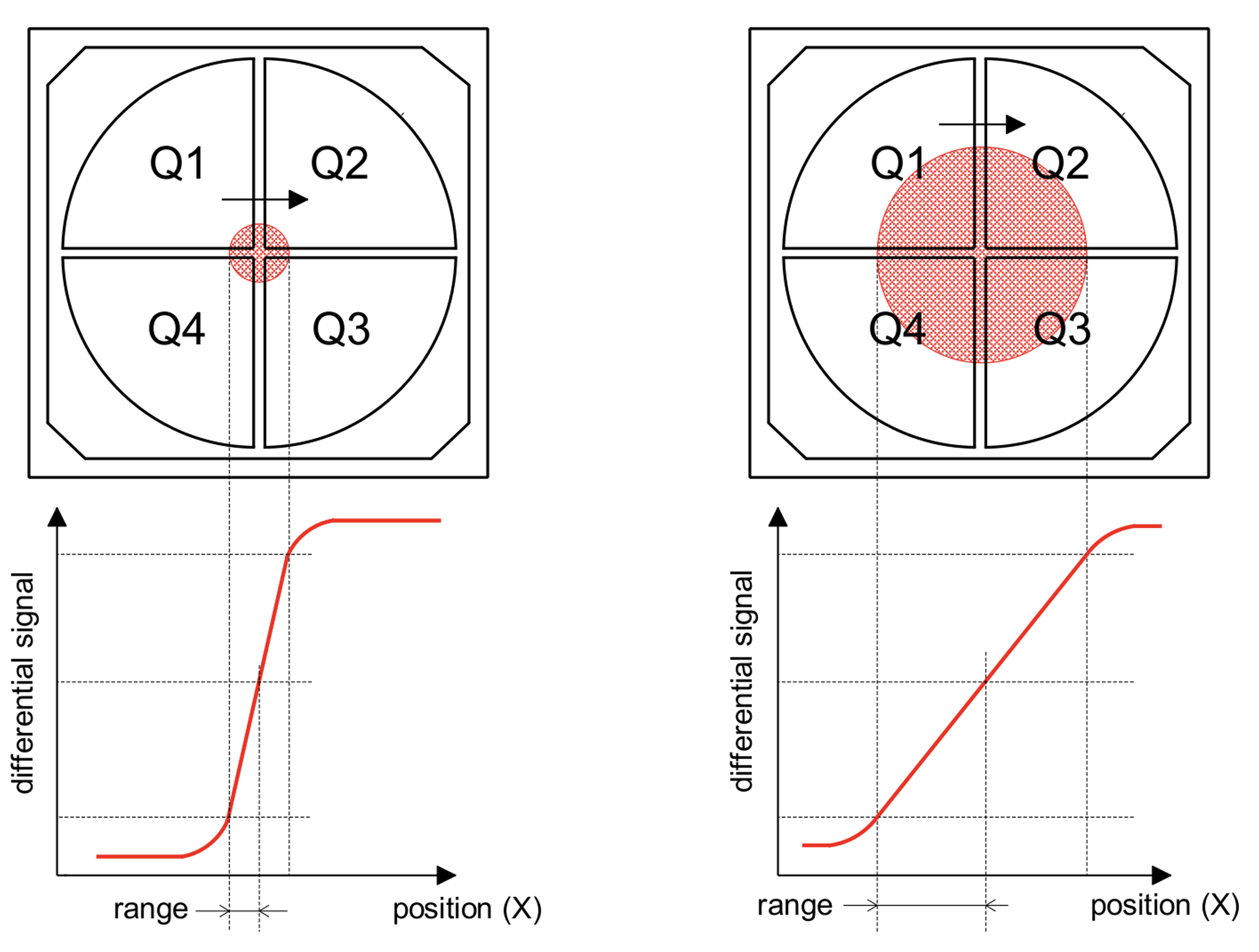
Trasduttore con fotodiodo a quadrante

• Un fascio laser illumina 4 fotodiodi disposti a quadrante
• La differenza tra le correnti generate tra fotodiodi affiancati è proporzionale allo spostamento del fascio in \(X\) e in \(Y\)
• Sensibilità molto elevata
• Corsa limitata
• Bassa linearità

Fotodiodo a quadrante

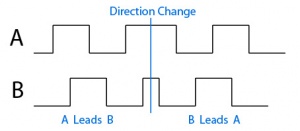
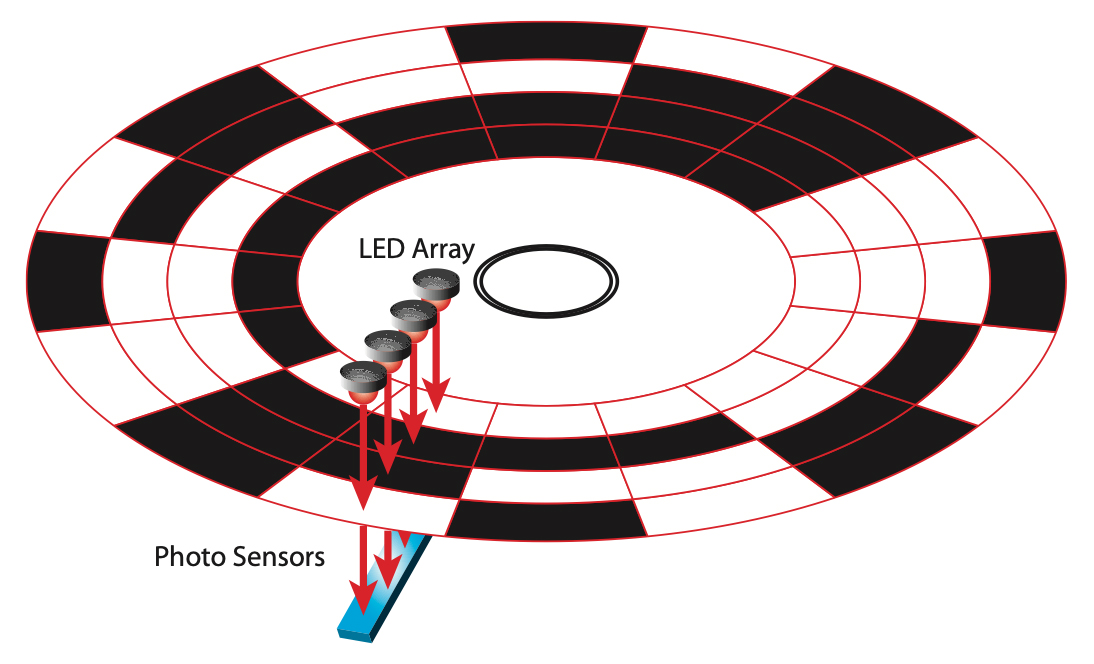
Encoder a riga ottica (relativi)

• Misurano uno spostamento rispetto a un riferimento per conteggio di una serie di impulsi
• Gli impulsi derivano da una griglia di alternanze (trasparente/opaco, poli N/S)
• Due griglie sfasate di 1/4 di periodo consentono di valutare la direzione di moto
• Risoluzione fino a 0.1 µm

Encoder a riga ottica (assoluti)

• Ogni posizione è identificata in maniera univoca da una sequenza di segnali binari (bianco/nero, N/S)
• Non serve un contatore e la misura è assoluta, non relativa a uno 0
• Serve un numero di detector \(n\) (segnali) che dipende dal numero di posizioni \(N\): \(n=\lceil\log_2(N)\rceil\)

Encoder assoluto (rotativo)

Nota

La notazione \(\lceil x \rceil\) indica l’arrotondamento all’intero superiore (ceiling)

Celle di carico e misure di forza

Da misure di deformazione a misure di forza

Principali metodi per misurare una forza

• Bilanciando la forza incognita contro la forza gravitazionale che agisce su una massa nota
• Misurando l’accelerazione di una massa nota sotto l’azione della forza incognita
• Bilanciando una forza magnetica che agisce contro la forza incognita
• Misurando il cambiamento di frequenza propria di un cavo messo in tensione dalla forza incognita
• Misurando la deformazione di un elemento elastico a cui si applica la forza incognita

Bilancia analitica

• Concettualmente semplice
• Può essere puramente meccanica
• Precisione dipende dalla qualità delle lavorazioni

Bilance analitiche

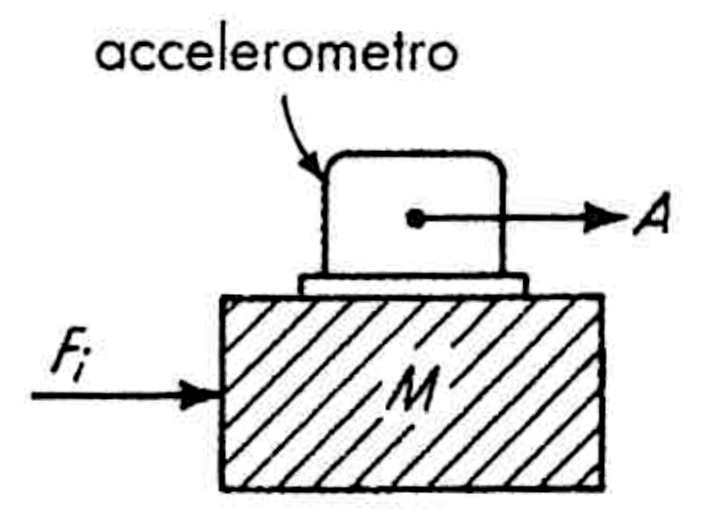
Trasduttore accelerometrico

• Da \(F=Ma\), nota la massa e misurando l’accelerazione si risale alla forza applicata
• È adatta a misure dinamiche, in cui la forza è variabile nel tempo
• Richiede l’accelerometro, che è a sua volta uno strumento di misura (con un trasduttore interno che misura uno spostamento o una deformazione di una massa nota)

Misura accelerometrica

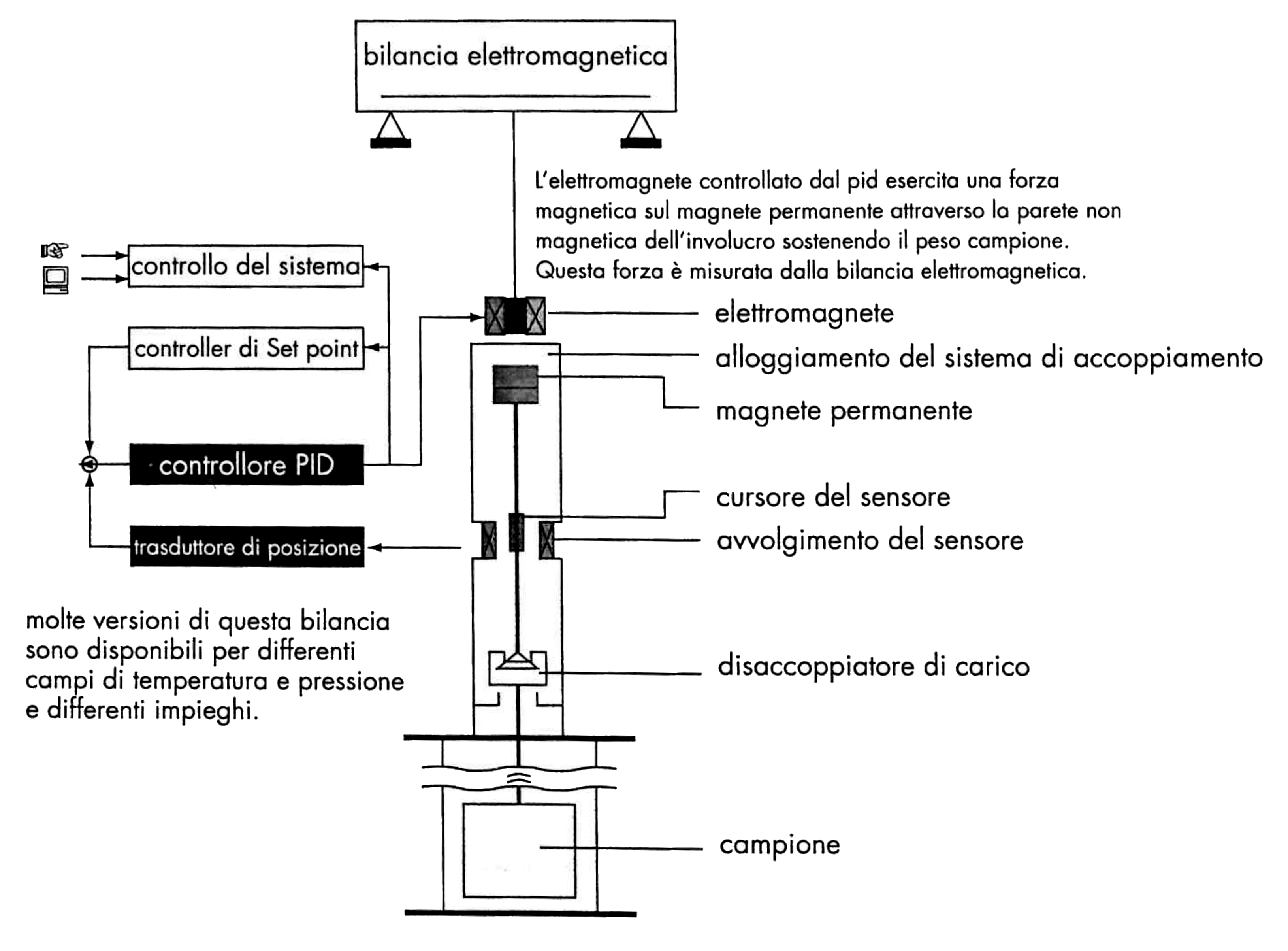
Bilancia elettromagnetica

• Sono basate su un trasduttore di posizione
• Lo scostamento rispetto a una posizione di riferimento è mantenuto nullo alimentando proporzionalmente un avvolgimento elettromagnetico
• La la corrente che alimenta l’avvolgimento è proporzionale alla forza incognita
• la bilancia può essere molto più compatta e più pronta delle bilance analitiche
• richiede un’alimentazione e un controllore

Bilancia elettromagnetica

Bilancia a vibrazione

• La frequenza di vibrazione di una corda tesa dipende dalla tensione
• Il trasduttore è un analizzatore di spettro, in grado di convertire un suono (vibrazione) in una misura di frequenza

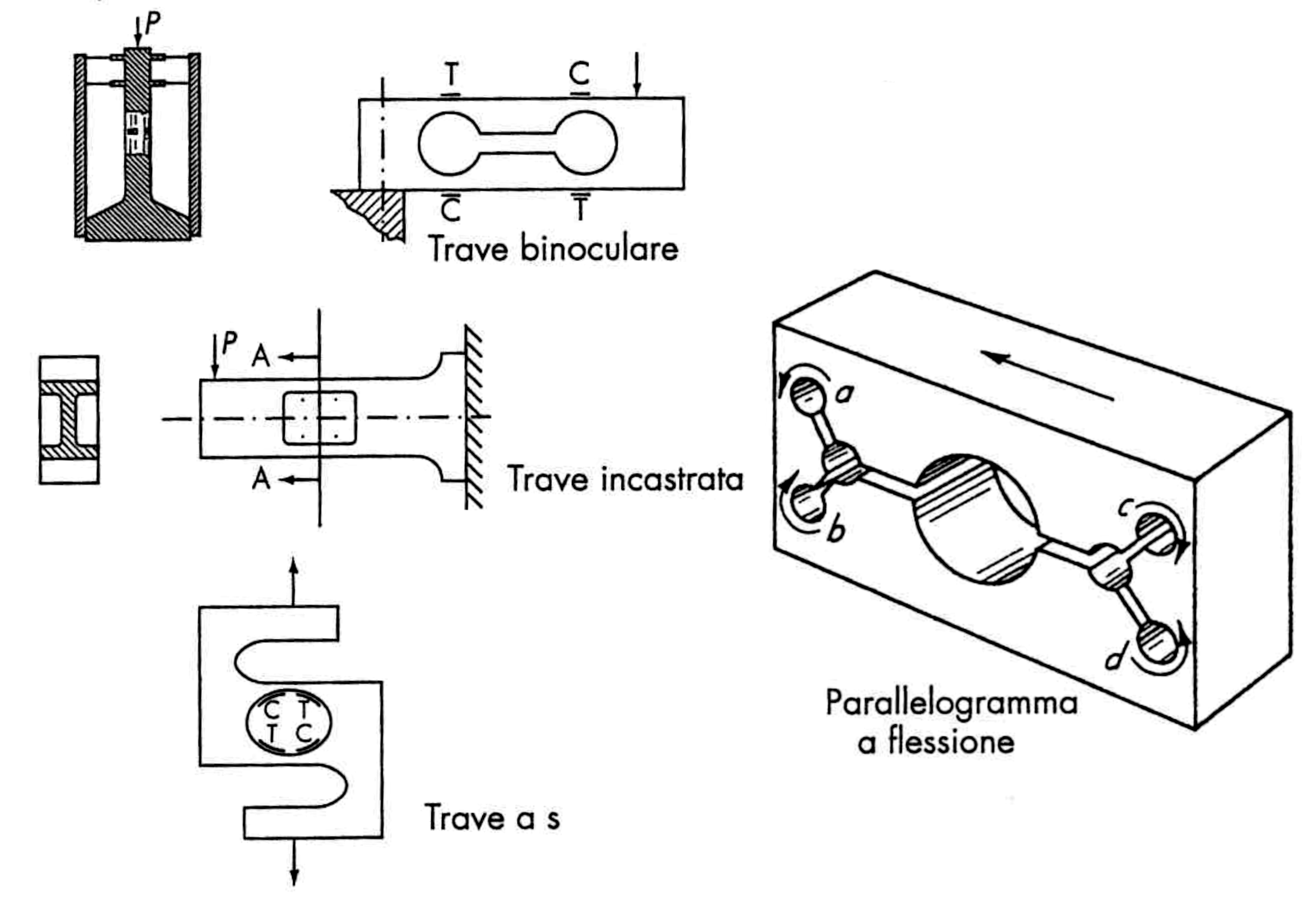
Dinamometro a elementi deformabili (cella di carico)

• Il trasduttore converte una deformazione meccanica in un segnale elettrico
• È adatto sia a misure statiche che a misure dinamiche
• È possibile compensare gli effetti interferenti e modificanti della temperatura

Celle di carico estensimetriche

Trasduttori di deformazione

Cioè come rilevare l’intensità della deformazione di un corpo

Sforzo e deformazione in campo elastico

In campo elastico la deformazione di un solido è reversibile e lineare

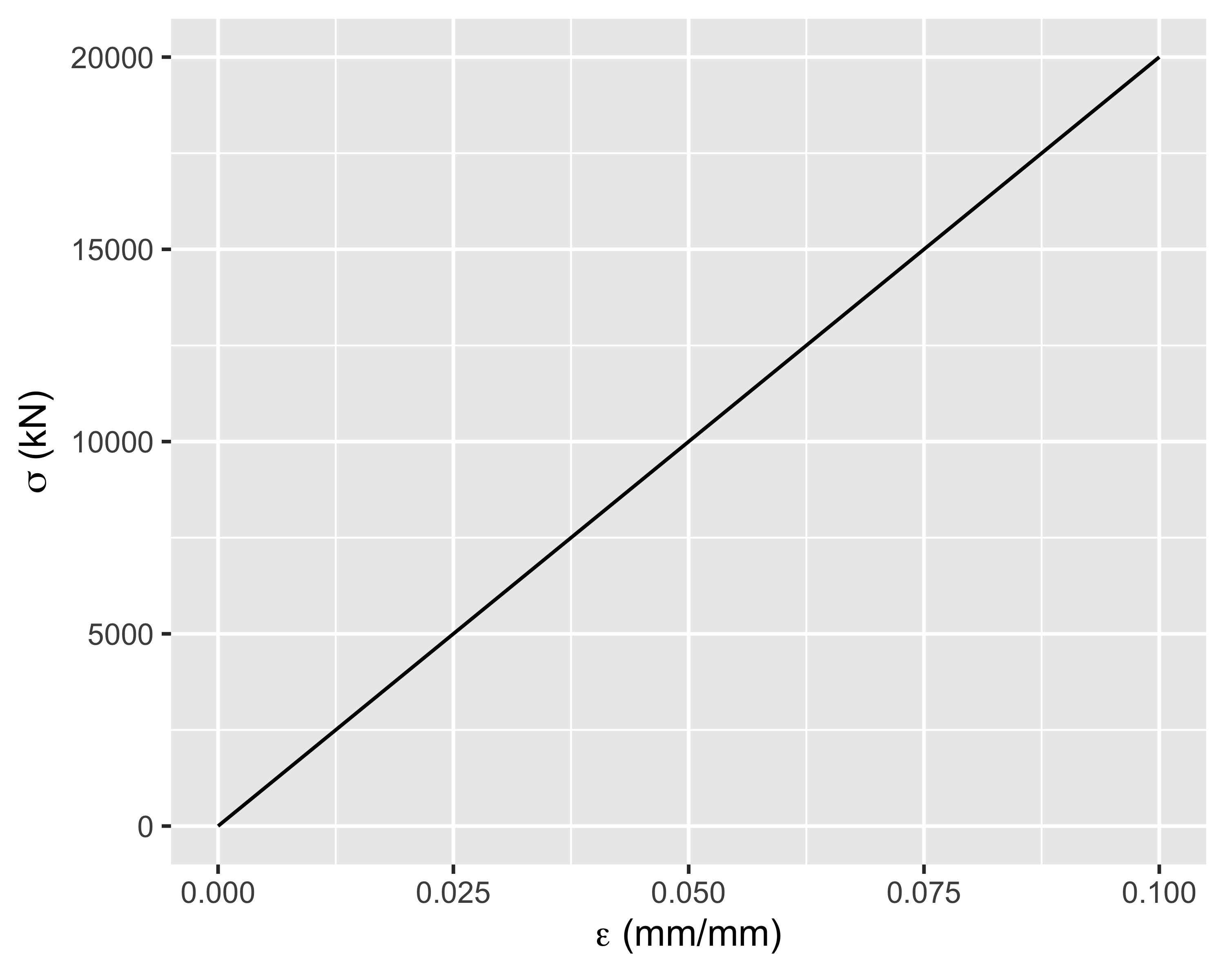
• Vale la legge di Newton: \(\sigma = E \varepsilon\) dove \(\sigma = F/A\) e \(\varepsilon=\Delta L / L_0\)
• \(E\) è il modulo di Young, o modulo elastico, ed è una proprietà del materiale
• La legge di Newton consente di misurare uno stato di sforzo a partire da uno stato di deformazione

Stati tensionali multiassiali

Sforzo e deformazione sono rappresentati da tensori: in ogni punto assumono valori nelle tre direzioni spaziali.

Ad esempio in 2-D:

Sforzi tensionali:

Deformazioni (\(\varepsilon\)): \[ \varepsilon_x = \frac{\sigma_x}{E}- \nu \frac{\sigma_y}{E},~~~\varepsilon_y = \frac{\sigma_y}{E}- \nu \frac{\sigma_x}{E} \] Quindi: \[ \sigma_x = \frac{E(\varepsilon_x + \nu\varepsilon_y)}{1-\nu^2},~~~ \sigma_y = \frac{E(\varepsilon_y + \nu\varepsilon_x)}{1-\nu^2} \]

Sforzo a taglio:

Sforzo (\(\gamma\)) e deformazione (\(\tau\)) di taglio \[ \gamma_{xy} = \frac{\tau_{xy}}{G} \]

Dove il modulo di taglio \(G\) è: \[ G=\frac{E}{2(1+\nu)} \]

Stati tensionali multiassiali

Quindi, se posso misurare lo stato tensionale (deformazioni), posso ricavare lo stato di sforzo (sollecitazione) e capire quanto un dato sistema è in sicurezza

La misurazione dello stato tensionale può essere

• puntuale, cioè localizzata su un’area/volume più piccolo possibile, tipicamente comparabile al grado di omogeneità del materiale
• media, cioè valutata su una lunghezza base elevata, in modo da mediare l’effetto di variazioni locali

Come si misurano

• Estensimetri meccanici (a leva meccanica): sono stati i primi ad essere sviluppati in ambito industriale, ma non avendo un accettabile rapporto tra livello di accuratezza e costi di realizzazione, sono stati soppiantati da altri tipi. Un altro limite è costituito dal fatto che gli elementi meccanici presentano inevitabilmente inerzia e attriti che non consentono di fare misure di deformazioni dinamiche
• Estensimetri ottici (a leva ottica, fotoelastici, interferometrici): garantiscono elevate accuratezze, ma a causa dell’elevato costo sono generalmente impiegati solo in laboratori metrologici
• Estensimetri acustici: usano il principio della corda vibrante, ovvero il fatto che una corda vibrante emette onde sonore a differente frequenza a seconda della tensione della corda
• Estensimetri elettrici a resistenza: i più diffusi e più economici, realizzabili in diverse dimensioni, generalmente di ottima accuratezza, con facile circuito di lettura

Trasduttore estensimetrico a resistenza

Sono basati su principio che l’allungamento di un conduttore provoca una aumento di resisteza proporzionale all’allungamento stesso

La sensibilità è aumentata ripiegando il conduttore su se stesso più volte

• Un estensimetro (strain gauge) fornisce una misura puntuale (mediata sulla lunghezza della patch)
• Un estensometro (extensometer) fornisce una misura media mediante un meccanismo a leve che deforma un estensimetro

Leggi dell’estensimetria

La resistenza elettrica è \(R=\rho L/A\), con \(L\) lunghezza, \(A\) sezione e \(\rho\) resistività

In termini di variazione:

\[\begin{align} \frac{\Delta R}{R} &= \frac{1}{R}\left( \frac{\partial R}{\partial\rho}\Delta \rho + \frac{\partial R}{\partial L}\Delta L +\frac{\partial R}{\partial A}\Delta A \right) = \frac{A}{\rho L}\left(\Delta \rho \frac{L}{A} + \Delta L \frac{\rho}{A} - \Delta A (\rho L)\right) \\ &=\frac{\Delta \rho}{\rho} + \frac{\Delta L}{L} - \frac{\Delta A}{A} \end{align}\]

Rappresentando l’area mediante un fattore di forma \(C\) e un parametro caratteristico \(D\) si ha:

\[ A=CD^2 \rightarrow \frac{\Delta A}{A} = 2\frac{\Delta D}{D} \rightarrow \frac{\Delta R}{R} = \frac{\Delta \rho}{\rho} + \frac{\Delta L}{L} - 2\frac{\Delta D}{D} \]

Leggi dell’estensimetria

Siccome \(\varepsilon_t = -\nu \varepsilon_l\), risulta che \(\Delta D/D = -\nu\Delta L/L\), e quindi:

\[ \frac{\Delta R}{R} = \frac{\Delta \rho}{\rho} + \frac{\Delta L}{L} - 2\left(-\nu\frac{\Delta L}{L}\right) = \frac{\Delta \rho}{\rho} + \frac{\Delta L}{L} (1 +2\nu) \]

Sostituendo \(\varepsilon_l = \Delta L/L\) si ha la prima legge dell’estensimetria:

\[\begin{align} \frac{\Delta R}{R} &= \varepsilon_l\frac{\Delta \rho}{\rho \varepsilon_l}+\varepsilon_l(1+2\nu) \\ &= \varepsilon_l\left(\frac{\Delta \rho}{\rho \varepsilon_l}+1+2\nu\right) =\varepsilon_l G_F \end{align}\]

Nota

• \(\Delta \rho/(\rho \varepsilon_l)\) è la sensibilità piezoresistiva (per metalli: \(s_p\simeq 0.4\)); non dipende da \(\varepsilon_l\)
• \(1 + 2\nu\) è la sensibilità geometrica (\(\nu \simeq 0.3\), quindi \(s_g \simeq 1.6\))
• \(G_F\) è il gauge factor

Effetto della temperatura

La temperatura ha effetto:

• interferente, perché la variazione di resistenza dovuta alla dilatazione termica e all’effetto termoresistivo (\(\rho=\rho(T)\)) si sommano alla misura
• modificante, perché la temperatura modifica il valore del gauge factor per via della sensibilità piezoresistiva \(\Delta \rho/(\varepsilon_l \rho)\)

Nota

Questi termini vanno compensati o automaticamente, o note le relazioni con la temperatura, e comunque sempre mediante controllo statistico (casualizzazione della sequenza)

Effetto interferente della temperatura

Effetto termoresistivo: la resistività \(\rho_T\) alla temperatura \(T\) è

\[ \rho_T - \rho_0= \rho_0\alpha_\rho \Delta T \] e quindi, in termini di variazione di resistenza rispetto alla temperatura di riferimento \(T_0\): \[ \Delta R_\rho = R(T) - R(T_0) = R_0\alpha_\rho\Delta T \]

Cioè: \(\frac{\Delta R_\rho}{R_0} = \alpha_\rho\Delta T\)

Nota

Il coefficiente \(\alpha_\rho\) è il coefficiente di sensibilità termica della resistività; la relazione può considerarsi lineare per variazioni modeste di temperatura (decina di gradi C)

Effetto interferente della temperatura

Effetto della dilatazione termica: la variazione di temperatura agisce dilatando sia l’estensimetro che il materiale, in modo potenzialmente differente. Ne consegue una deformazione dell’estensimetro:

\[ \Delta L_{\Delta T} = L_0 (\alpha_m - \alpha_g)\Delta T\rightarrow\frac{\Delta L_{\Delta T}}{L_0}=\varepsilon_{\Delta T}=(\alpha_m - \alpha_g)\Delta T \]

In termini di variazione di resistenza associata:

\[ \frac{\Delta R_{\Delta L}}{R_0} = G_F(\alpha_m - \alpha_g)\Delta T \] Combinando:

\[ \frac{\Delta R_{\Delta T}}{R_0} = \frac{\Delta R_{\Delta L}}{R_0} + \frac{\Delta R_\rho}{R_0} = \left(\alpha_\rho + G_F(\alpha_m - \alpha_g) \right)\Delta T \]

Autocompensazione

Dato che:

\[ \frac{\Delta R_{\Delta T}}{R_0} = \left(\alpha_\rho + G_F(\alpha_m - \alpha_g) \right)\Delta T \]

in certi casi è possibile scegliere un materiale dello strain gauge (e quindi un valore di \(\alpha_g\)) tale che sia

\[ G_F(\alpha_m - \alpha_g)\approx\alpha_\rho \] e, quindi, risulti \(\frac{\Delta R_{\Delta T}}{R_0} \approx 0\)

Nota

In questo caso lo strain gauge si dice autocompensato in temperatura

Effetto modificante della temperatura

• L’effetto modificante è connesso alla dipendenza dalla temperatura del termine piezoresistivo che compare nella formula del fattore di taratura \(G_F\)
• I materiali comunemente adottati per gli estensimetri elettrici a resistenza, e in particolare la costantana, manifestano un ridotto contributo piezoresistivo al fattore di taratura, di conseguenza anche l’effetto modificante non ha rilevanza nell’impiego a temperatura ambiente, in particolare indicata con \(T_0=24^\circ\mathrm{C}\) per un campo di temperature compreso in \(\pm25^\circ\mathrm{C}\) rispetto \(T_0\), l’eventuale correzione da apportare al fattore di taratura è minore del 0.5% e quindi solitamente dello stesso ordine di grandezza dell’incertezza con cui è noto tale parametro
• La compensazione dell’effetto \(G_F=G_F(T)\) viene calibrata empiricamente dal costruttore che fornisce la sensitività \(\beta\) in: \[ G_F(T) = G_{F,0} (1 - \beta(T- T_0)) \]

Misura della variazione di resistenza

• Le misure differenziali sono sempre preferibili perché danno maggiore sensibilità
• Nel circuito a ponte di Wheatstone se le resistenze sono tutte uguali il ponte è detto bilanciato e \(V_\mathrm{out}=0\)
• In generale vale:

\[ V_\mathrm{out} = \frac{V_\mathrm{in}}{4}\left( \frac{\Delta R_1}{R_1} - \frac{\Delta R_2}{R_2} + \frac{\Delta R_3}{R_3} - \frac{\Delta R_4}{R_4}\right) \]

Ponte di Wheatstone

Nota

Cioè: variazioni su rami adiacenti si sottraggono; variazioni su rami opposti si sommano!

Misura della variazione di resistenza: quarto di ponte

Se una delle 4 resistenze è un estensimetro resistivo:

\[ V_\mathrm{out} = \frac{V_\mathrm{in}}{4}\left( \frac{\Delta R_1}{R_1}\right) = \frac{V_\mathrm{in}}{4}G_F\varepsilon_l \]

Ponte di Wheatstone

Misura della variazione di resistenza: mezzo ponte

Se sue resistenze adiacenti sono ER, la seconda può compensare la temperatura:

\[ V_\mathrm{out} = \frac{V_\mathrm{in}}{4}\left( \frac{\Delta R_1}{R_1} - \frac{\Delta R_2}{R_2}\right) \] Se sue resistenze opposte sono ER, la combinazione aumenta la sensibilità:

\[ V_\mathrm{out} = \frac{V_\mathrm{in}}{4}\left( \frac{\Delta R_1}{R_1} + \frac{\Delta R_3}{R_3}\right) \]

Ponte di Wheatstone

Misura della variazione di resistenza: ponte intero

Si usano 4 ER, a due a due compensati in temperatura e raddoppiando la sensibilità

\[ V_\mathrm{out} = \frac{V_\mathrm{in}}{4}\left( \frac{\Delta R_1}{R_1} - \frac{\Delta R_2}{R_2} + \frac{\Delta R_3}{R_3} - \frac{\Delta R_4}{R_4}\right) \]

Ponte di Wheatstone

Dinamometro a mensola

Nell’esercizio sul dinamometro a mensola si è usata l’espressione: \[ V=3/2GV_i\frac{lG_F}{EBH^2}F+V_0 \] Per una trave snella la deformazione massima è: \[ \varepsilon_l = \frac{6l}{EBH^2}F \]

Dinamometro a mensola

e per il quarto di ponte si ha (con \(V_i=GV_\mathrm{in}\) e \(V_0\) che è la tara): \[\begin{align} V_\mathrm{out} &= \frac{V_\mathrm{in}}{4}\left( \frac{\Delta R_1}{R_1}\right) = \frac{V_\mathrm{in}}{4}G_F\varepsilon_l \\ \frac{V}{V_\mathrm{in}} &= \frac{\varepsilon_l}{4}G_F = \frac{6l}{4EBH^2}F G_F = 3/2\frac{lG_F}{EBH^2}F \end{align}\]

Digitalizzazione

Cioè conversione di un segnale analogico in digitale

Digitalizzazione di un segnale

• Il trasduttore generalmente produce un segnale debole che va condizionato prima possibile
• Cioè, va collegato con cavi schermati di qualità e più corti possibile ad un convertitore/amplificatore
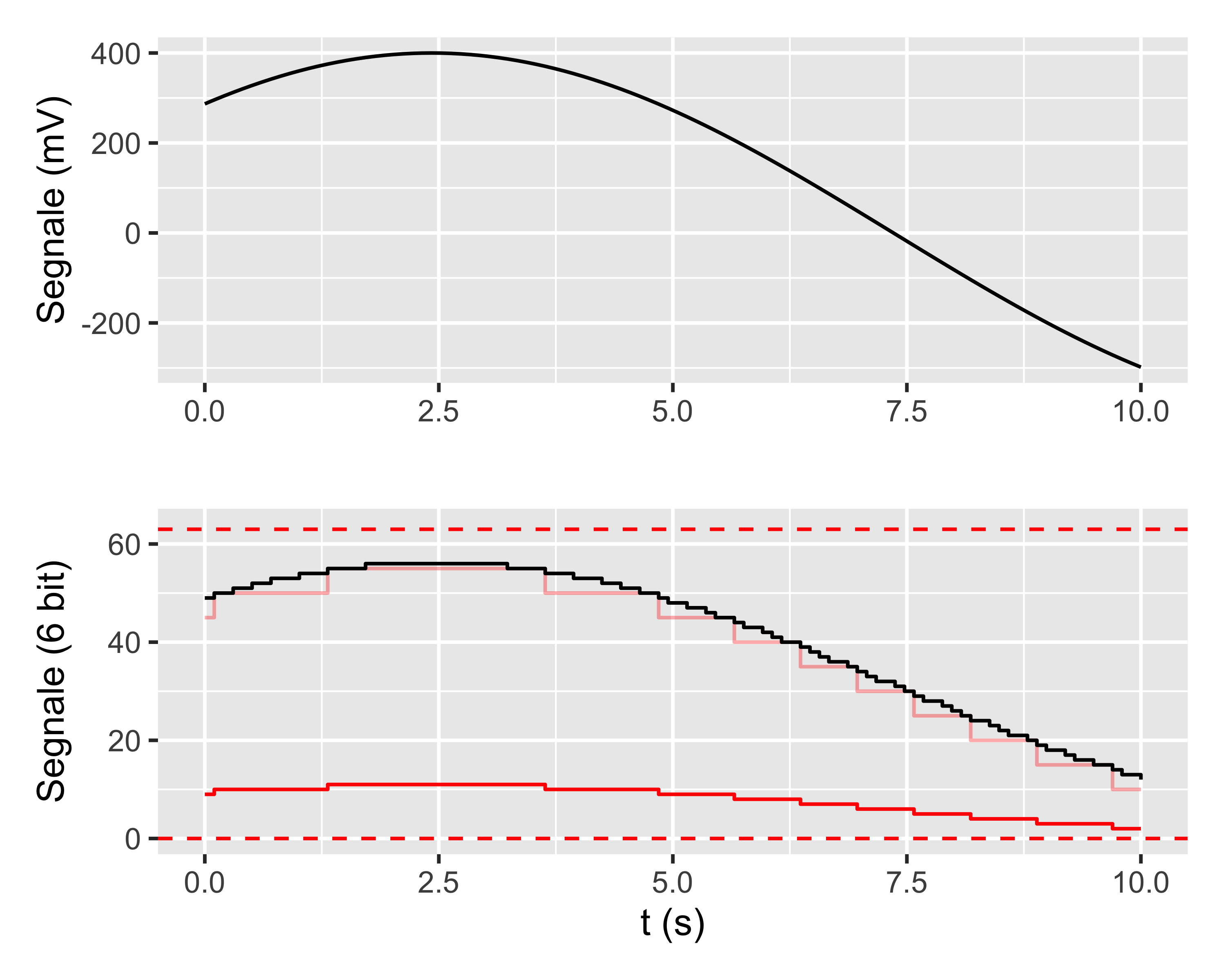
• Il segnale amplificato (in tensione o in corrente) va digitalizzato cioè convertito in un valore su scala discreta, e codificato, cioè rappresentato in valore numerico
• Il numero di bit del convertitore dà il numero di livelli: es. 8 bit significa 256 livelli

Per massimizzare le prestazioni è importante calibrare il guadagno dell’amplificatore in modo da sfruttare il più possibile la gamma dinamica del convertitore, perché viceversa l’amplificazione sul segnale digitale rende più evidente la quantizzazione (serie in rosso)